Co je to logika?
-
Logika je věda o správném usuzování
-
Logika studuje formy usuzování bez ohledu na obsah, proto má moderní logika symbolický charakter
-
Moderní logika bývá označována jako logika formální (symbolická)
-
Klasická logika = logika, která používá dvě pravdivostní hodnoty (pravda a nepravda) a klasické logické spojky
-
Neklasické logika = logika, která se zabývá dalšími aspekty
- Modální logika - používá neklasické spojky (“je možné, že”, “je nutné, že”)
- Temporální logika - zabývá se tvrzeními, ve kterých hraje roli čas
- Fuzzy logika - studuje více pravdivostních hodnot
-
Znalost základů logiky nám umožňuje srozumitelně a jednoznačně se vyjadřovat a argumentovat
Výroky a logické spojky
-
Výrok je tvrzení (výpověď), u kterého má smysl uvažovat o jeho pravdivosti
-
Logické spojky jsou jazykové výrazy, kterými z jednodušších výroků vytváříme výroky složitější
-
Výrok může mít
- Pravdivostní hodnotu 1 (“pravda”)
- Pravdivostní hodnotu 0 (“nepravda”)
-
Pravdivostní hodnotu výroku V označujeme
- e = pravdivostní ohodnocení
-
Pravdivostní hodnota výroku se počítá z pravdivostních hodnot atomických výroků pomocí pravdivostních funkcí spojek
| Název | Symbol | Pravdivostní funkce | Tabulka pravdivostní funkce |
|---|---|---|---|
| Negace | ㄱ | ㄱ’ | 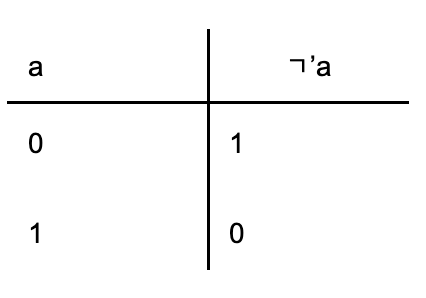 |
| Konjunkce | ⋀ | ⋀’ | 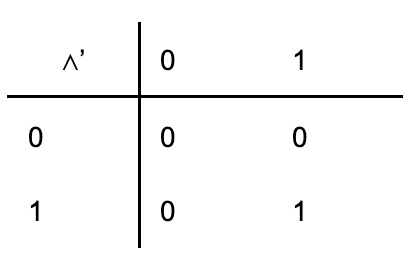 |
| Disjunkce | ⋁ | ⋁‘ | 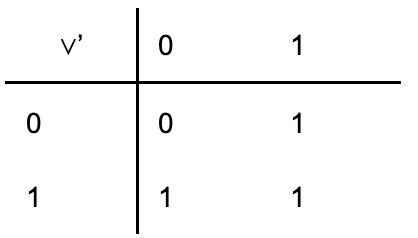 |
| Implikace | ⟶ | ⟶‘ | 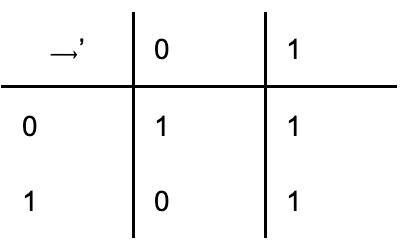 |
| Ekvivalence | ↔ | ↔‘ | 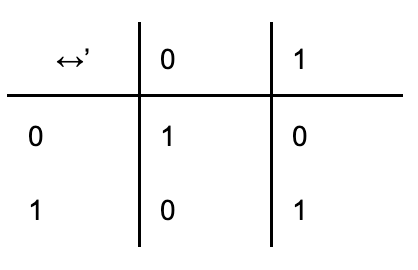 |
| Piercova | ↓ | ↓‘ | 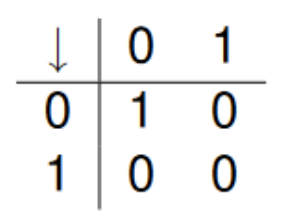 |
| Shefferova | ↑ | ↑‘ | 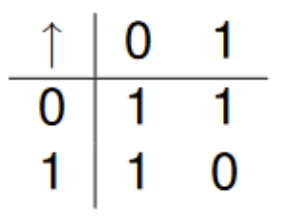 |
Výroky s proměnou, kvantifikátory
-
Některé výrazy přirozeného jazyka obsahují proměnné
- Číslo x je větší nebo rovno 3
-
Tyto výrazy nejsou výroky. Museli bychom určit hodnotu proměnných, které se v těchto výrazech vyskytují.
-
Výrazy obsahující proměnné, ze kterých se po dosazení hodnot za proměnné stanou výroky, nazýváme výrokové formy
-
Výrokové formy bývají zvykem označovat písmenem, za kterým jsou v závorce uvedeny všechny proměnné, které forma obsahuje
- Číslo x je větší nebo rovno 3 =
-
Kvantifikátory jsou jazykové výrazy, kterými z výrokových forem vznikají výroky
Obecný kvantifikátor
- Symbolicky jej značíme
- Symbol pochází z němčiny ze slova allgemein (obecný)
- Je pravdivý, pokud pro všechny hodnoty z oboru hodnot je výrok pravdivý
- Použití pro výrokovou formu “x je větší nebo rovno 1”:
- Pro každé x platí, že x je větší nebo rovno 1
- () ( je větší nebo rovno 1)
- () ()
Existenční kvantifikátor
- Symbolicky jej značíme
- Symbol pochází z němčiny ze slova existentiell (existenční)
- Je pravdivý, pokud pro alespoň jednu hodnotu z oboru hodnot je výrok pravdivý
- Použití pro výraz “x je větší nebo rovno 1”:
- Existuje tak, že je větší nebo rovno 1
- ( je větší nebo rovno 1)
Základy výrokové logiky
-
Výroková logika je nejjednodušším formálním systémem logiky
-
Ve výrokové logice nepracujeme s výroky samotnými, ale pracujeme s formami výroků
-
Formy výroků se nazývají formule a jsou to přesně definované řetězce symbolů
-
Konkrétní výroky dostaneme nahrazením výrokových symbolů atomickými výroky
-
Formule jsou jisté posloupnosti symbolů jazyka, samy o sobě nemají žádný význam
-
Jazyk výrokové logiky se skládá z:
- výrokových symbolů - p, q, r, …
- symbolů výrokových spojek - ㄱ, ∧, ∨, ⟶, ↔
- pomocných symbolů - různé druhy závorek
-
Formule daného jazyka výrokové logiky je definovaná následovně:
- každý výrokový symbol je formule (tzv. atomické)
- jsou-li φ (phi) a 𝜓 (psi) formule, jsou i formule (tzv. složené) i výrazy:
- ㄱφ
- (φ ∧ 𝜓)
- (φ ∨ 𝜓)
- (φ ⟶ 𝜓)
- (φ ↔ 𝜓)
-
Pravdivostní ohodnocení je libovolné zobrazení výrokových symbolů daného jazyka výrokové logiky do množiny
-
0 a 1 reprezentují nepravda a pravda
-
Pravdivostní hodnota formule φ při ohodnocení , označujeme ji , je definována:
- Je-li výrokovým symbolem , pak
- = e(p)
- Je-li složená formule, pak
- =
- Je-li výrokovým symbolem , pak
-
Tautologie = je-li formule při každém ohodnocení pravdivá
-
Kontradikce = je-li formule při každém ohodnocení nepravdivá
-
Splnitelná = je-li formule alespoň při jednom ohodnocení pravdivá
-
Formule sémanticky plyne z formule , značíme , jestliže je pravdivá při každém ohodnocení, při kterém je pravdivá
-
Pokud sémanticky plyne z a naopak, říkáme, že a jsou sémanticky ekvivalentní
Navigace
Předchozí: Je první hehe Následující: Booleovské funkce, funkčně úplné systémy Celý okruh: 1. Teoretické základy informačních technologií