Hashovací tabulky, metody řešení kolizí

Hashovací tabulka

• Zobecnění pole:
  • Rozdíl je ve způsobu adresování.
  • Místo množiny klíčů $\{0,1,2,...,m-1\}$, které jsou vlastně indexy do pole, máme obecnou množinu klíčů $U$.
• Hlavní idea: Hashovací funkce $h:U\to \{0,1,...,m-1\}$ pro přepočet obecného klíče na index v tabulce.

Úvod do hashovacích tabulek

Implementace

struct table
	data:[]key //pole klíčů
	hash-function //hashovací funkce

Kostra přístupu k místu, kde je v tabulce $T$ klíč $k$

• Počítáme index: $i\leftarrow T.\text{hash-function}(k)$
• Přistoupíme k prvku: $T.\text{data}[i]$

Kolize

• Pro množinu klíčů $U$, velikost tabulky $m$ a hashovací funkci $h$ kolize nastane pokud: existují klíče $k_1,k_2\in U,$ tak že $k_1\ne k_2,$ ale $h(k_1)=h(k_2)$.
• Kolize určitě nastane, pokud $\mid U\mid >m$: to plyne z Dirichletova principu
• I když máme $\mid U\mid <m,$ může být pravděpodobnost, že dojde ke kolizi, vysoká (narozeninový paradox)

Řešení kolizí pomocí řetězení (chaining)

• Klíče, které se zahashují na stejný index ukládáme do seznamu

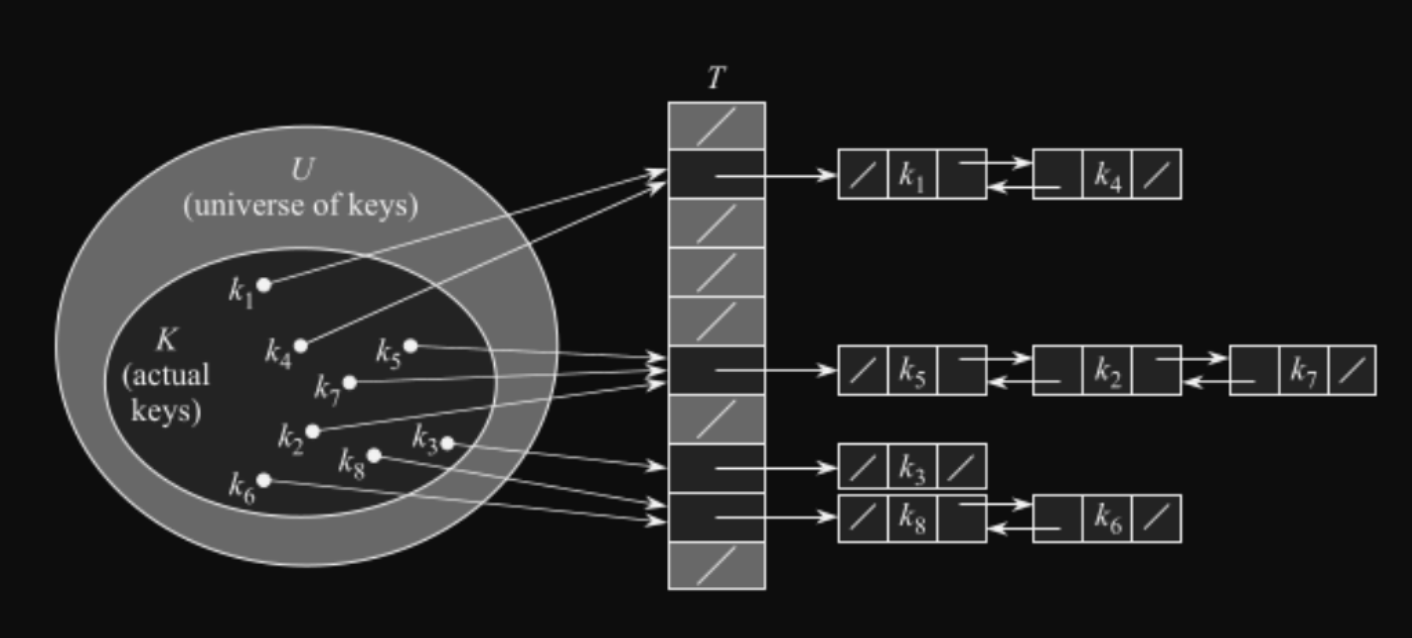
Implementace

struct table
	data:[]list 
	hash-function

//Argumenty T = table, k = key
proc insert(T,k)
  index = h(k)
  list-insert(T[index], x)

proc delete(T, k)
  index = h(k)
  list-delete(T[index], x)

proc search(T,k)
  index = h(k)
  list-search(T[index], k)

Složitost v nejhorším čase

• Složitost insert a delete zůstávají konstantní.
• Složitost search může být v nejhorším případě lineární
  • všechny klíče prvků v tabulce zobrazili pomocí $h$ na stejnou hodnotu, nebo se klíč v tabulce nenachází

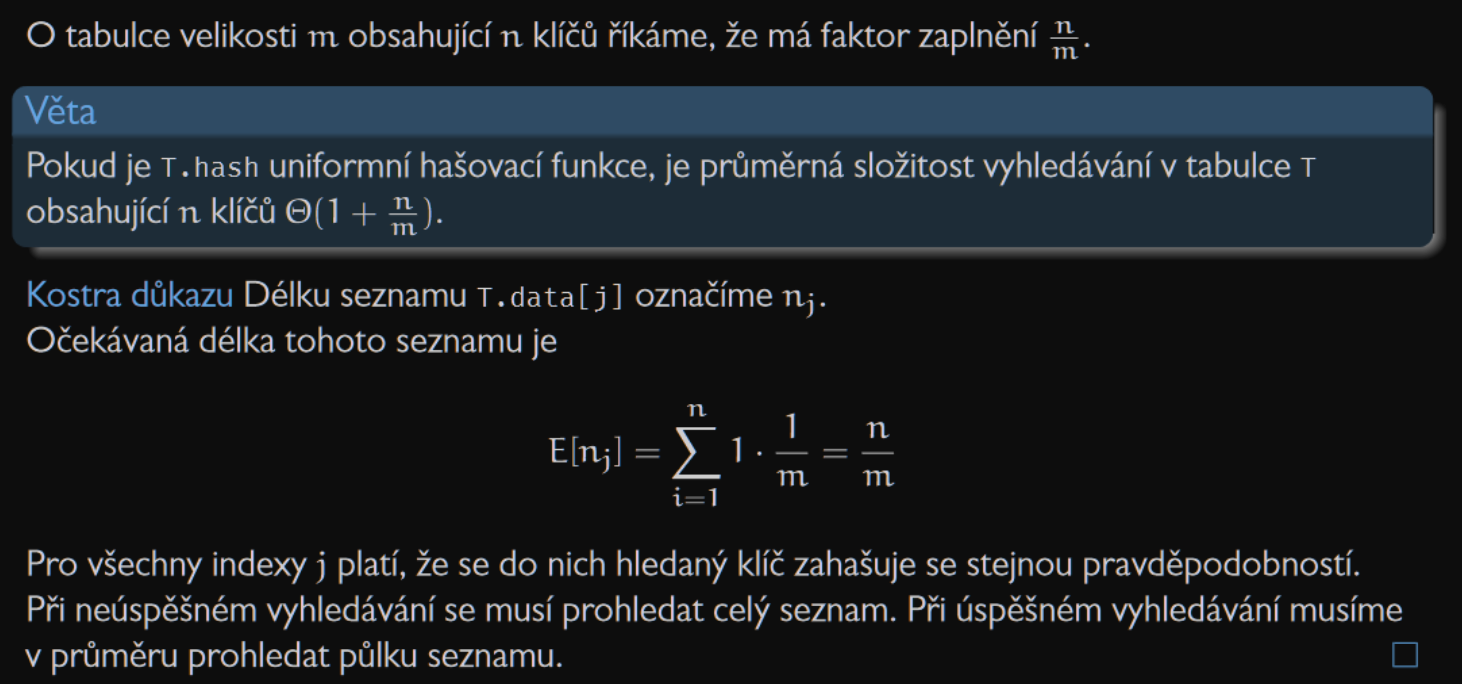
Složitost search v průměrném případě

Konstrukce hashovací funkce

• Cíl je jednoduché rovnoměrné hashování

• Potřebujeme znalost rozložení pravděpodobnosti při výběru klíče a nezávislost (= výběr jednoho klíče nezmění pravděpodobnosti výběru dalších klíčů)

• Nejlepší co můžeme udělat je, aby hashovací funkce moc nezávisela na vzorech, vyskytujících se v datech.

• Používáme heuristiky, jejichž cílem je, aby výsledek funkce závisel na všech částech klíče

• Příklad závislosti na vzoru v datech:

  • Klíče jsou celá čísla, $k=2,h(k)=k\text{ mod }2$
    • Problém je, že výsledek závisí pouze na jednom bitu klíče.
    • Aby funkce dobře fungovala, musíme předpokládat, že je stejně pravděpodobné, že klíč bude lichý jako že klíč bude sudý

Obecný postup konstrukce

• Klíč $k$ bereme jako posloupnost číslic v nějaké číselné soustavě
  • např. jako posloupnost bajtů = číslic v soustavě o základu $256$
• Hashovací funkce má obvykle $2$ fáze:
  • sekvenci čísel použijeme pro výpočet hodnoty, která ovšem může být větší než $m-1$
  • hodnotu z předchozího bodu upravíme tak, aby byla mezi $0$ a $m-1$

Příklad

Tip

U dělící metody není dobré, když je velikost tabulky mocnina $2$, protože pak výsledek záleží pouze na hodnotě spodních bitů (jejich počet odpovídá exponentu)

Metoda řešení kolize: Otevřené adresování

• Prvky jsou v samostatné tabulce (neobsahuje seznamy prvků), prázdná políčka jsou nil

• Velikost tabulky omezuje počet prvků, které se do tabulky vejdou (faktor zaplnění tabulky není nikdy větší než $1$)

• Pro účel vyhledávání a vkládání používáme průzkumné posloupnosti.

• Vytvoříme průzkumnou funkci:

  • $g:U\times \{0,1,...,m-1\}\to \{0,1,...,m-1\}$

• Platí pro ni, že $g(k,i)\ne g(k,j)\text{ pro vsˇechny }k\in U\text{ a }i\ne j\in \{0,1,...,m-1\}$

• Průzkumná posloupnost pro klíč $k$ je potom $g(k,0),g(k,1),...,g(k,m-1)$

Princip otevřeného adresování

• Při vyhledávání indexu odpovídajícího klíči $k$ prohledáváme tabulku v pořadí odpovídající průzkumné posloupnosti pro $k$.
  • Pokud je na aktuálním indexu klíč různý od $k$, pokračujeme v průzkumné posloupnosti dál.
  • Pokud je na aktuálním indexu nil, klíč se v tabulce nenachází.
  • Pokud projdeme celou průzkumnou posloupnost, klíč se v tabulce nenachází.
• Analogický postup použijeme pro přidávání uzlu: uzel přidáme na první index z průzkumné posloupnosti, na kterém je nil.
• Odstranění prvku z tabulky by způsobilo přerušení průzkumné posloupnosti při vyhledávání. Prvky v tabulce proto musíme ponechat, ale dát jim příznak, že jsou smazány. Potom musíme příslušným způsobem upravit procedury pro přidávání (přidáváme i na místo, kde je smazaný prvek) a prohledávání (smazané prvky přeskakujeme).
• Složitost těchto operací pak ale nezávisí přímo na faktoru zaplnění tabulky. Pokud potřebujeme i operaci mazání, je lepší použít řetězení.

Lineární prozkoumávání

• Máme hashovací funkci $h$. K ní vytvoříme průzkumnou funkci $g(k,i)=(h(k)+i)\text{ mod }m$

• Průzkumná posloupnost tedy začíná $h(k)$ a pak lineárně projdeme zbytek políček tabulky stejně, jako bychom procházeli pole (s tím, že když se dostaneme na konec tabulky, začneme znovu od začátku)

• Navštívím všechna políčka

• Existuje $m$ různých průzkumných posloupností

• Problém je primární shlukování: vzniknou dlouhé úseky obsazených políček, které tak zvyšují průměrný čas nutný k vyhledávání

Kvadratické prozkoumávání

• Máme hashovací funkci $h$. K ní vytvoříme průzkumnou funkci $g(k,i)=(h(k)+c_{1}i+c_2{i}^2)\text{ mod }m$

  • $c_1,c_2$ jsou vhodně zvolené konstanty

• Pro některou kombinaci hodnot $c_1,c_2$ a $m$ nemusí $g$ být průzkumná funkce (máme $i\ne j$ takové, že $g(k,i)=g(k,j))$ (Je těžké trefit dokonalou kombinaci $c_1,c_2$ a $m$)

• Pokud je např. $m$ prvočíslo, pak většina voleb $c_1,c_2$ (např. $1,1$ nebo $0,1$). vede k tomu, že délka průzkumné posloupnosti před tím, než narazíme na opakující se hodnotu, je přibližně $\frac{m}{2}$

• Vzniká sekundární shlukování - pokud máme $k_1\ne k_2$, ale $h(k_1)=h(k_2)$, mají $k_1$ a $k_2$ stejné průzkumné sekvence.

• Existuje $m$ různých průzkumných posloupností

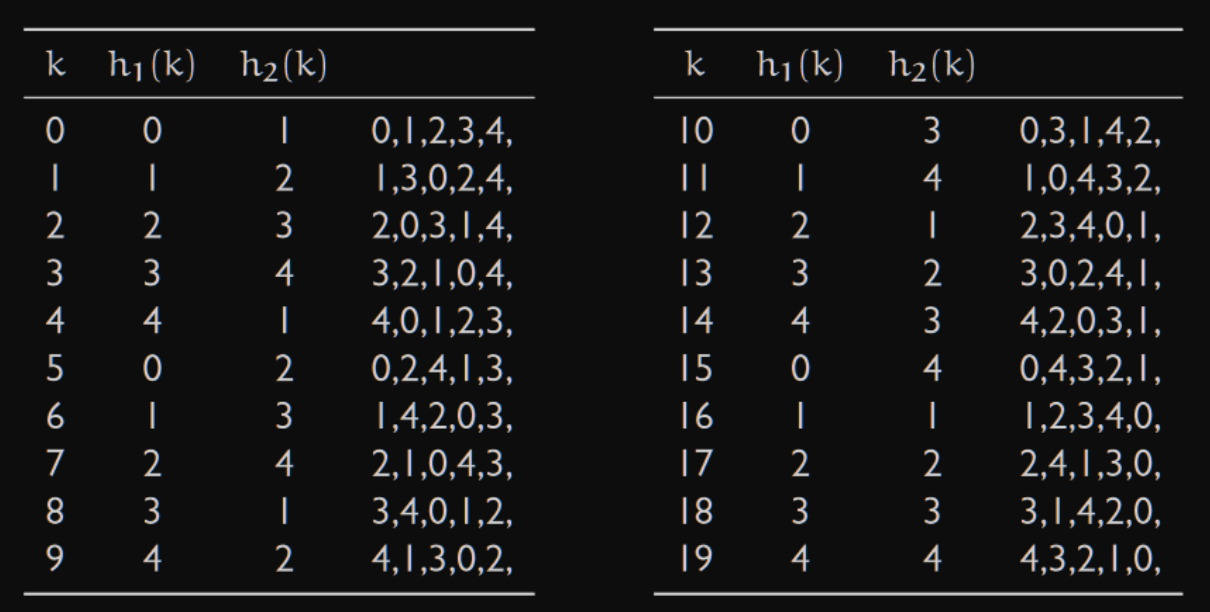
Příklady průzkumných posloupností

• Předpokládejme, že $h(k)=0$.
  • $m=7,c_1=0,c_2=1$ $0,1,4,2,2,4,1$
  • $m=11,c_1=1,c_2=1$ $0,2,6,1,9,8,9,1,6,2,0$
  • $m=7,c_1=13,c_2=15$ $0,0,5,1,2,1,5$
  • $m=16,c_1=0.5,c_2=0.5$ $0,1,3,6,10,15,5,12,4,13,7,2,14,11,9,8$

Dvojité hashování

• Pro hashovací funkce $h_1,h_2$ zavedeme průzkumnou funkci $g(k,i)=(h_1(k)+i{h}_2(k))\text{ mod }m$

• Hashovací funkce $h_1$ určuje počáteční pozici, hashovací funkce $h_2$ určuje offset, o který se posouváme

• Aby $g$ byla prohledávací funkce, musí být $h_2(k)$ a $m$ nesoudělné. Můžeme zvolit:

  • $m$ jako prvočíslo
  • $h_1(k)=k\text{ mod }m$
  • $h_2(k)=1+(k\text{ mod }m-1)$

• Pro prvočíselné $m$ existuje $m^2$ průzkumných posloupností

Příklad pro m=5

Navigace

Předchozí: B stromy, operace a jejich složitost Následující: Základní grafové algoritmy - průchod do šířky, průchod do hloubky, topologické uspořádání Celý okruh: 1. Teoretické základy informačních technologií