- Konečné automaty nacházejí velmi široké uplatnění v technické praxi. Z hlediska efektivity a nákladnosti implementace je důležité, aby počet stavů byl pokud možno co nejmenší. Přirozeným problémem je proto konstrukce minimálního automatu, který rozpoznává daný regulární jazyk .
- Minimální automat lze sestrojit poměrně jednoduchým způsobem - stačí mít k dispozici nějaký konečný automat, který rozpoznává . Minimální automat pak obdržíme ztotožněním některých jeho stavů.
Nerozlišitelnost stavů
-
Stavy v DFA A nazveme nerozlišitelné, právě když pro platí
-
Nerozlišitelnost stavů "" je binární relace na množině stavů , která je navíc ekvivalence
- Pro každé platí
- reflexivní: je nerozlišitelné s
- symetrická: když je nerozlišitelné s , tak je nerozlišitelné s
- tranzitivní: když je nerozlišitelné s a je nerozlišitelné s , pak je nerozlišitelné s
- Pro každé platí
-
Pro stavy výsledného minimálního DFA platí, že jsou to třídy a množina stavů tvoří rozklad podle (předpokládáme, že nemá nedosažitelné stavy)
Postup
- Minimální DFA lze vypočítat pomocí tabulky dvojic stavů, která zachycuje
- Nejprve označíme všechny dvojice, které obsahují pouze jeden koncový stav
- (Ty jsme schopni rozlišit hned na začátku)
- Postupně označujeme dvojice , pro které existuje takové, že dvojice už je označena
- Tento krok opakujeme dokud ještě lze označit nějakou další dvojici
- Neoznačené dvojice nejsme schopni rozlišit a pomocí tranzitivního uzávěru vypočítáme celou odpovídající třídu , kterou v sloučíme do jednoho stavu
Příklad
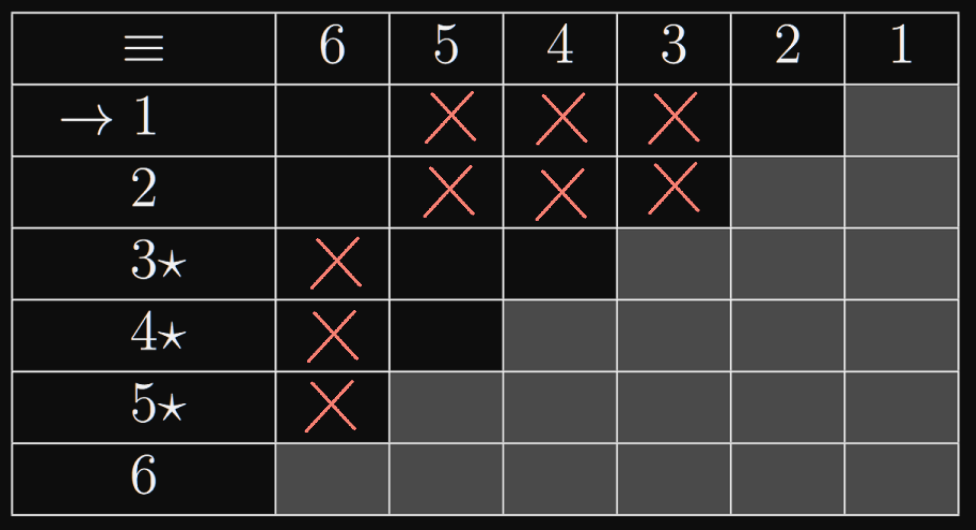
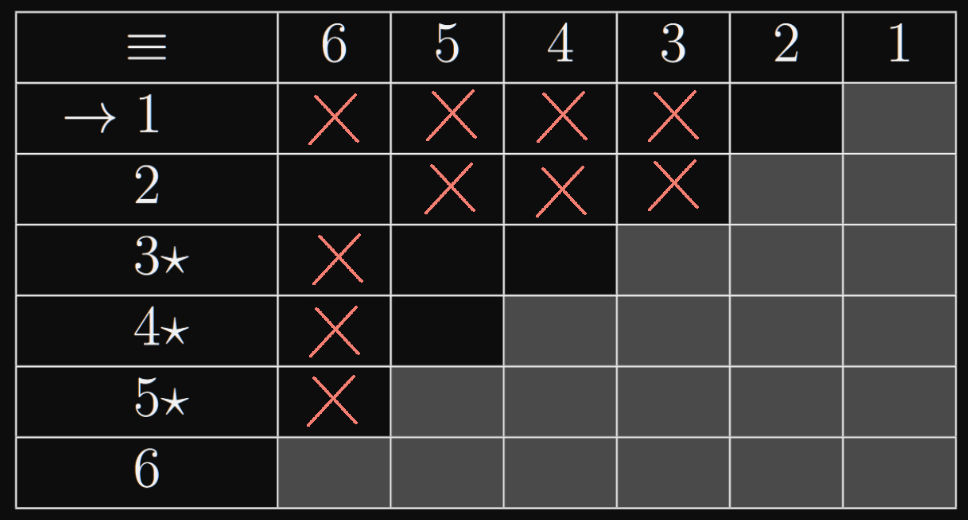
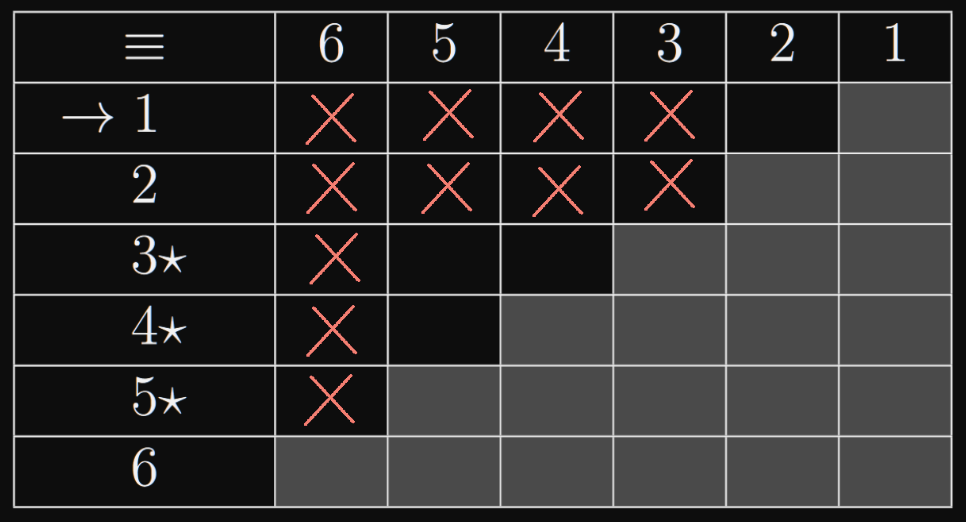
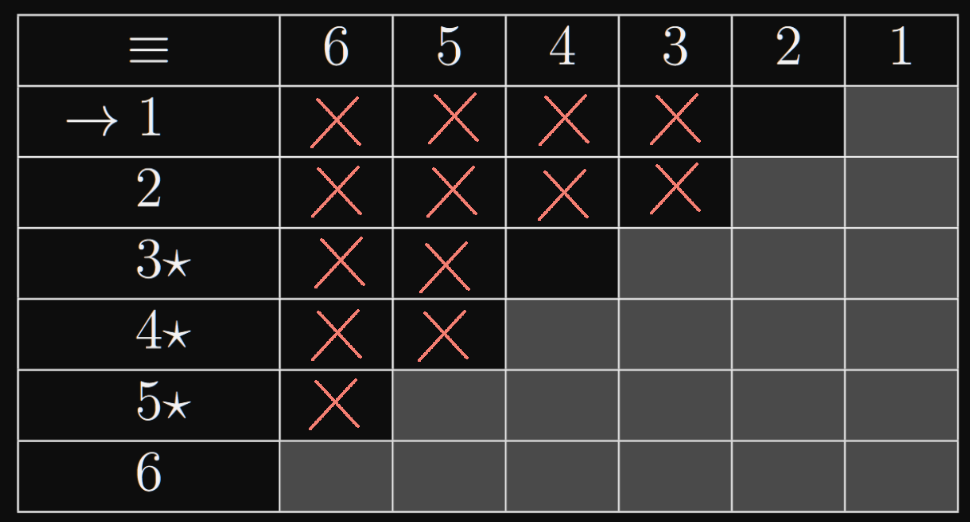
- minimalizujte DFA zadaný tabulkou
- Označím dvojice takové, že
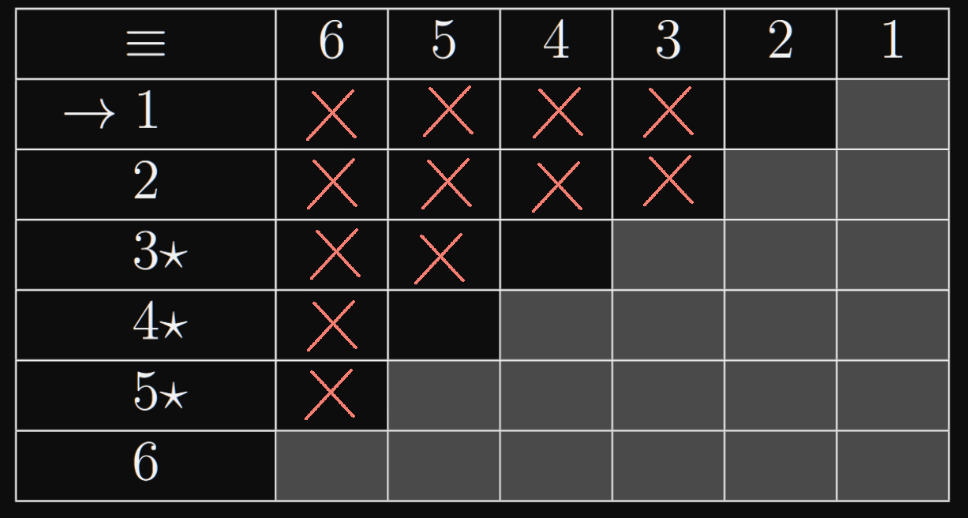
- Můj postup: Kouknu na volné místa (např. u dvojice ) a kouknu do tabulky, jaké dvojice by museli být označeny, abych mohl označit danou dvojici (tabulka říká buď nebo . A zkontroluju jestli taková není už zaškrtlá (dvojici nemáme, ale dvojici máme zaškrtlou, takže můžu zašktnout i ). Když pro nějakou ještě nemám zašktnutou dvojici, tak počkám na konec, může se ještě objevit.)
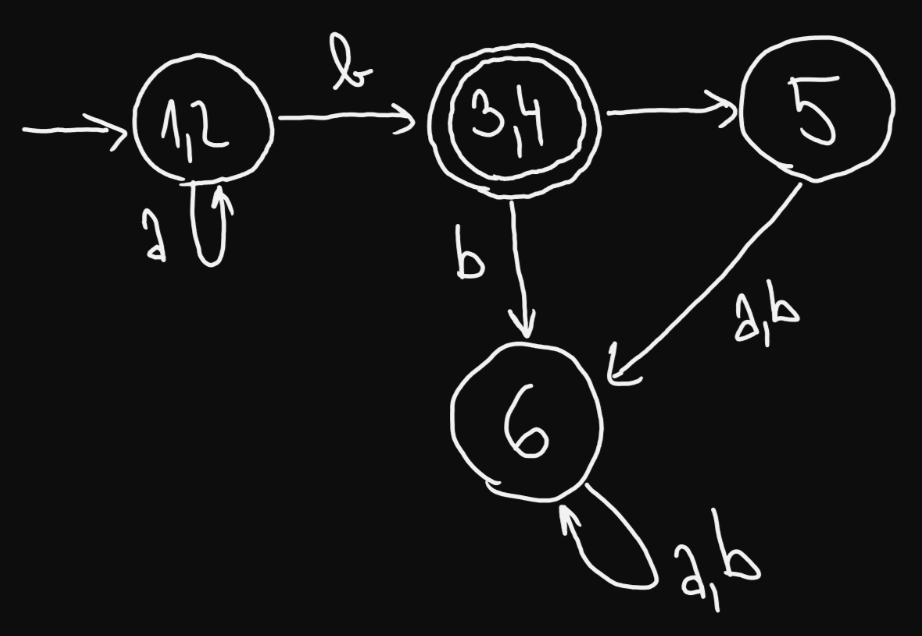
- Dvojice a jsou pro nás nerozlišitelné. Tedy výsledný automat je:
Navigace
Předchozí: Regulární výrazy, automaty s e-přechody Následující: Pumping lemma Celý okruh: 1. Teoretické základy informatiky