Primitivní funkce
- Nechť je definována na intervalu libovolného druhu.
- Potom máme funkci takovou, že platí - *pokud zderivuji funkci dostanu funkci - nazýváme *primitivní funkcí k na
O primitivní funkci
- Nechť je primitivní funkce k na . Pak také funkce definovaná předpisem , , je primitivní funkcí k na .
- Nechť a jsou primitivní funkce k funkci na , pak funkce , je konstantní.
- Tato nejednoznačnost primitivní funkce k vede k definici neurčitého integrálu
Neurčitý integrál funkce na
- Nechť existuje alespoň jedna primitivní funkce k funkci na intervalu .
- Množinu všech primitivních funkcí k funkci na pak nazýváme neurčitý integrál funkce na a značíme jej
- Primitivních funkcí k funkci je nekonečně mnoho a liší se pouze konstantou
- jde o tzv. *integrační konstantu
- to je dáno tím, že při derivaci funkce se vyloučí veškeré konstanty
- Po integraci funkce na je vhodné tuto konstantu pro úplnost doplnit
- (po získání primitivní funkce k - opačná operace k derivaci)
- Značení:
- - značení integrálu
- - integrovaná funkce (integrand)
- - proměnná podle které integrujeme (integrační proměnná)
- - primitivní funkce
- - integrační konstanta
Isibalo - Co nám říká neurčitý integrál
O existenci primitivní funkce
- Nechť je spojitá na intervalu libovolného druhu, pak má na primitivní funkci.
- Funkce , která není na R spojitá, nemusí mít na R primitivní funkci
O linearitě primitivní funkce
- Nechť na existují primitivní funkce k funkcím a a nechť . Pak existuje primitivní funkce k funkci a platí
- Větu o linearitě lze zobecnit na tvar
Metody výpočtu neurčitého integrálu
- Na rozdíl od derivace, integrace žádná přesně definovaná pravidla pro počítání složitějších výrazů nemá
- K tomu se využívá různých metod
- per-partes (typicky pro výrazy obsahující součin)
- substituce (složené funkce)
- Typicky se snažíme převést integrovaný výraz do ekvivalentní podoby, kterou integrovat umíme
Přímá integrace
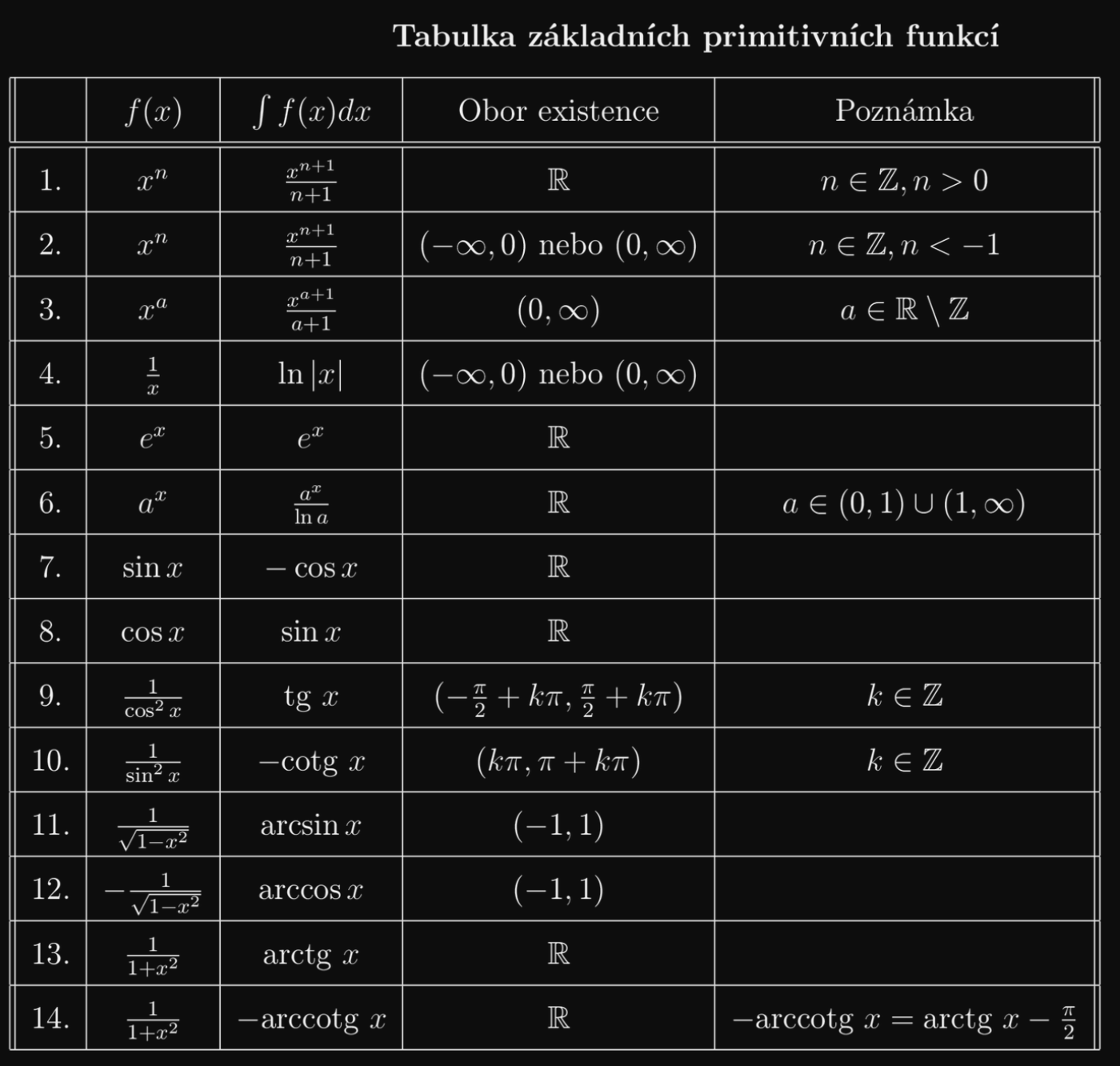
- Převádíme integrál na primitivní funkci pomocí tabulky základních primitivních funkcí, větě o linearitě a vzorečku 1. jednotlivé součty ve výrazu rozdělíme na samostatné integrály 2. vytkneme konstanty před integrály 3. jednotlivé integrály spočítáme podle pravidel pro primitivní funkce (dle tabulky níže) - pro složitější výrazy je nutné využít substituce, per partes apod.
Metoda per partes (“po částech”)
- Nechť funkce jsou definovány na a nechť a na .
- Nechť dále existuje na . Pak také existuje na a platí
- Tvrzení věty si budeme lépe pamatovat ve tvaru
- Možná čitelnější zápis:
- Odvozeno z pravidla pro derivaci součinu funkcí - - obě strany zintegrujeme - - tedy nebo
- Tato metoda je vhodná, když je jedna funkce v součinu snadno diferencovatelná a druhá integrovatelná
Isibalo - Metoda per partes
Substituční metoda
- Převádíme složenou funkci, kterou neumíme integrovat do jednoduššího tvaru tak, aby šla integrovat přímo
- Volba vhodné substituce není snadná a vyžaduje nějakou zkušenost
Isibalo - Substituční metoda
První věta o substituci
- Nechť funkce zobrazuje interval do intervalu a nechť na existuje vlastní .
- Nechť funkce má na intervalu primitivní funkci , tj. platí , . Pak na existuje primitivní funkce k funkci a platí
neboli
- Postup výpočtu neurčitého integrálu pomocí první věty o substituci:
- Hledáme integrál tvaru .
- Pokud funkce a splňují podmínky první věty o substituci, pak:
a) Položíme , , .
.
b) Vypočítáme integrál ,
- doufáme, že je výraz jednodušší než původní integrál v zadání a umíme ho spočítat
- Vrátíme se k proměnné a hledaný neurčitý integrál má tvar , .
- Stručněji:
Druhá věta o substituci
- Nechť funkce zobrazuje interval na interval a nechť na existuje vlastní (nebo ).
- Nechť je primitivní funkce k funkci na intervalu , tj. platí , . Pak na existuje primitivní funkce k funkci a platí neboli
- Postup výpočtu neurčitého integrálu pomocí druhé věty o substituci:
- Hledáme integrál tvaru
- Zvolíme nějakou vhodnou funkci a pokud funkce a splňují podmínky druhé věty o substituci, pak
a) položíme , , ,
b) vypočítáme integrál
- opět doufáme, že nový výraz je jednodušší než původní integrál v zadání a umíme ho spočítat
- Vrátíme se k proměnné a hledaný neurčitý integrál má tvar Stručněji:
Integrace racionálních funkcí
- Je třeba umět integrovat následující čtyři typy zlomků:
- ,
- ,
- ,
- ,
kde , a .
- Výpočet jednotlivých případů:
-
pro pak
-
Je-li a (čitatel je tak derivací jmenovatele), pak máme obecně
-
Pokud máme obecně a , pak
- Potom je
-
Nakonec vyřešíme nejobecnější případ třetího typu zlomku. Při výpočtu tohoto integrálu použijeme to, co již známe ze speciálních tvarů v předchozích dvou příkladech.
-
Obecně vypadá úprava a postup takto:
-
Tyto integrály jsme však postupně vyřešili výše.
- Pomocí substituce
Navigace
Předchozí: Průběh funkce - základní věty diferenciálního počtu, extrémy funkce, konvexní a konkávní křivky, asymptoty Následující: Riemannův určitý integrál - definice, základní věta integrálního počtu, metody výpočtu Celý okruh: 1. Teoretické základy informačních technologií