-
Datové struktury = Způsob uložení entit, které se vyskytují v programu do paměti
- entita = jakákoliv přesně definovaná množina dat
-
Lineární datové struktury
- Prvky jsou seřazeny do posloupnosti (má smysl uvažovat o pořadí prvků)
- U každého prvku známe předka a následníka (pokud existují)
Lineární vyhledávání (Linear search)
- Lineární vyhledávání je nejjednodušší vyhledávací algoritmus, který prochází každý prvek datové struktury jeden po druhém, dokud nenalezne hledaný prvek nebo neprojde celou strukturu.
- Výhody:
- Jednoduchá implementace.
- Nevyžaduje žádné předpoklady o uspořádání dat.
- Nevýhody:
- Pomalejší pro velké datové sady ve srovnání s efektivnějšími algoritmy.
Pole
-
Prvky jsou v paměti uspořádány za sebou
-
K prvkům přistupujeme pomocí indexu v čase (konstantním čase)
-
Má fixní velikost (alternativa dynamické pole)
-
Všechny prvky jsou stejného typu
-

-
Výpočet přístupu k -tému prvku:
struct array-set{
data, //pole prvků node
top, //index místa pro zápis
cap //velikost pole data
}
//nebezpečí overflow
proc insert(AS, x) Θ(1)
AS.data[AS.top] = x
AS.top += 1**
//nebezpečí underflow
proc delete(AS, i) Θ(1)
AS.top -= 1
AS.data[i] = AS.data[AS.top] 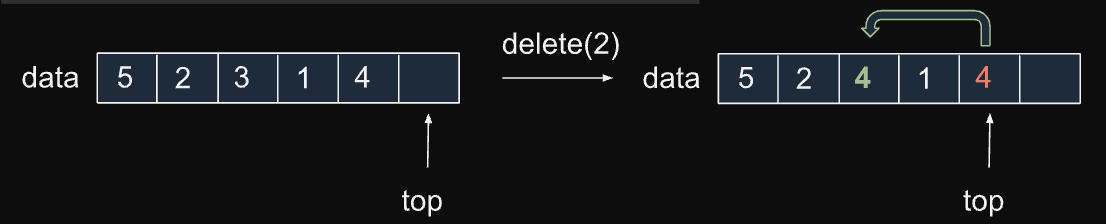
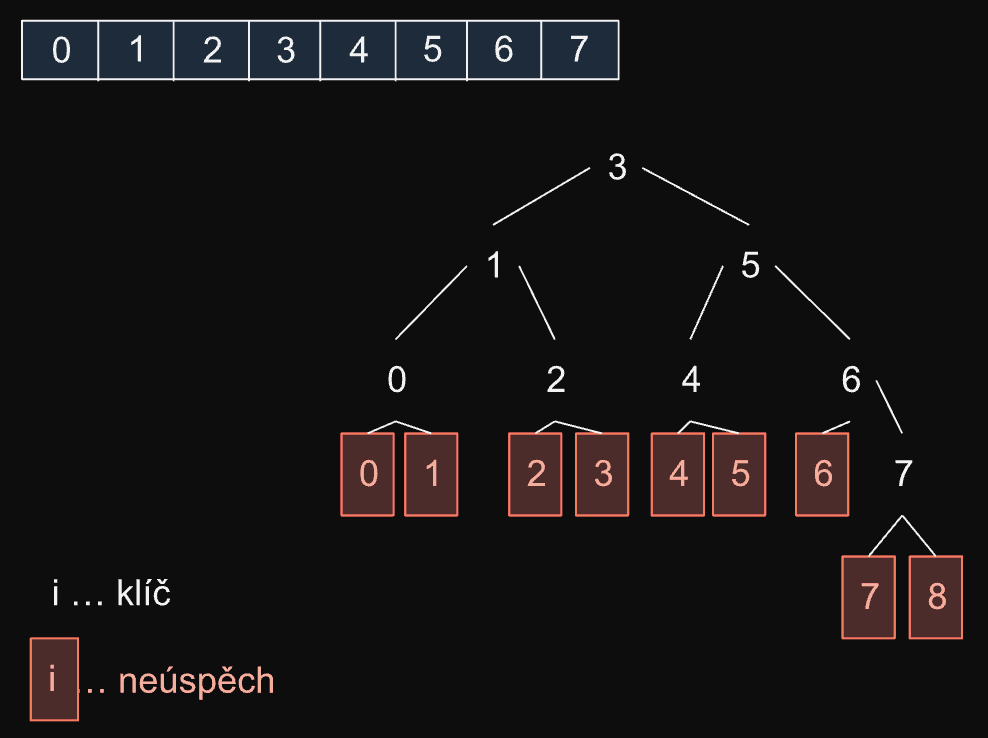
Vyhledávání v nesetřízeném a setřízeném poli
1. V nesetřízeném poli
proc search(A,k)
for i = 0; i < n; i++
if A[i].key == k then return i
return -1- Zrychlení drobným trikem, za cenu zmenšení kapacity o :
proc search-alt(A,k)
AS.data[AS.top] = k
for i = 0; true; i++
if AS.data[i].key == k then return i- Složitost
search(A,k)- Sledujeme počet porovnání v závislosti na velikosti pole
- Nejhorší případ = Prvek s klíčem se v nenachází. Projdeme celé pole a složitost je
- Průměrný případ = Pokud se prvek s klíčem v poli nachází, pak je počet porovnání
- předpokládáme, že všechny prvky v poli vyhledáváme stejně často
2. V setřízeném poli
- Předpokládejme, že klíče bereme z úplně uspořádané množiny (čísla, lexikálně uspořádané řetězce, …)
- Při neúspěšném vyhledávání v setřízeném poli potřebujeme nejhůře tolik porovnání, jako při vyhledávání v nesetřízeném poli, jsou ale případy, kdy potřebujeme méně
proc search(A,k)
for i = 0; i < n and A[i].key <= key; i++
if A[i].key == k then return i
return -1- Složitost = V nejhorším případě (Kdy je vyhledávaný prvek na konci pole, nebo je větší než všechny ostatní prvky v poli) je stále
Binární vyhledávání
- Idea:
- Při hledání prvku s klíčem se podíváme na prostřední prvek pole , řekněme, že je na indexu .
- Pokud je
k == A[s].keyvyhledávání je úspěšné - Pokud
k < A[s].key, rekurzivně vyhledáváme v části pole ohraničeném indexy - Pokud
k > A[s].key, vyhledáváme v části pole ohraničeném indexy
- Složitost )
proc binary-search(A,k)
l = 0
p = n - 1
while l <= p
s = floor((l + p)/ 2)
if A[s].key == k then return s
if A[s].key > k
p = s - 1
else
l = s + 1
return -1Setřízené pole převedeme na tzv. strom vyhledávání
Příklad
Interpolační vyhledávání
- Algoritmus je vylepšením binárního vyhledávání pro případy, kdy jsou hodnoty v seznamu nejen seřazené, ale zároveň rovnoměrně rozložené.
- Složitost
- V nejhorším případě ovšem může být složitost až . Aby se zabránilo nejhoršímu případu, je možné kombinovat interpolační vyhledávání s binárním vyhledáváním (například střídat vždy jeden krok interpolačního vyhledávání a jeden binárního vyhledávání)
Příklad
- Tuto metodu intuitivně používají lidé například při vyhledávání ve slovníku - odhadnou, kde by přibližně mohlo hledané heslo být (např. heslo začínající písmenem “K” bude pravděpodobně někde před polovinou slovníku) a otevřou slovník na odhadnutém místě. Podle odchylky postupují dopředu nebo dozadu o menší nebo větší počet stránek.
- Jako příklad budeme uvažovat seznam čísel . Pokusíme se najít prvek . Pokud bychom hledali pomocí binárního vyhledávání, prvním testovaným prvkem by bylo číslo , poté číslo a nakonec námi hledané číslo . Interpolační vyhledávací algoritmus odhadne pozici a přímo přejde na prvek .
Vizualizace interpolačního vyhledávání
Fibonacciho posloupnost vyhledávání
-
Fibonacciho posloupnost vyhledávání je vyhledávací algoritmus, který funguje na principu binárního vyhledávání, ale místo dělení pole na dvě stejně velká podpole se pole dělí na dvě podpole, jejichž velikost odpovídá dvěma po sobě jdoucím číslům Fibonacciho posloupnosti.
-
Algoritmus začne s celým polem a dvěma ukazateli: jeden na začátku pole a druhý na konci pole. Poté se vypočte nejbližší číslo Fibonacciho posloupnosti, které je větší nebo rovno velikosti pole. Toto číslo určuje délku prvního podpole. Algoritmus porovná hledanou hodnotu s prvkem na konci tohoto podpole. Pokud je hledaná hodnota menší, pole se zmenší na první polovinu, jinak se pole zmenší na druhou polovinu. Tento postup se opakuje, dokud se hledaná hodnota nenajde nebo dokud se pole nezmenší na velikost jednoho prvku.
-
Fibonacciho vyhledávání má složitost , což z něj dělá rychlejší než lineární vyhledávací algoritmy, ale pomalejší než binární vyhledávání. Jeho výhoda spočívá v tom, že je efektivní pro velká pole, zejména pokud jsou data uložena v pomalé paměti, protože algoritmus umožňuje minimalizovat počet přístupů k paměti. Fibonacciho vyhledávání se však v praxi často nepoužívá, protože je složitější než binární vyhledávání a jeho výhody jsou často zastíněny moderními vyhledávacími algoritmy s ještě lepšími výsledky.
Navigace
Předchozí: Pořádkové statistiky Následující: Binární vyhledávací stromy, operace a jejich složitosti Celý okruh: 1. Teoretické základy informačních technologií