O-notace a růst funkcí, definice, vlastnosti, příklady použití

• O-notace je způsob popisu růstu funkcí v informatice a matematice.
• Je zásadní pro analýzu algoritmů, zejména pro hodnocení jejich efektivity z hlediska času a paměťové náročnosti, když velikost vstupu roste do nekonečna.
• O-notace popisuje, jak rychle roste funkce s porovnání s jinou funkcí, když se její vstup (obvykle velikost dat) stává velmi velkým.

Základní pojmy pro porovnání růstu funkcí

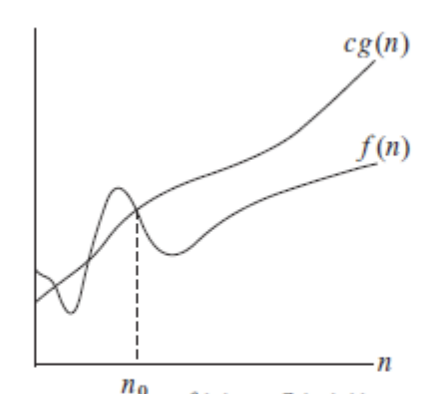
• $O(g)$ … Asymptotická horní mez

  • používána se pro popis horního limitu růstu funkce
  • $O(g(n))=\{f(n)\mid (\exists c\in \mathbb{N})(\exists n_0\in \mathbb{N})(\forall n\ge n_0):0\le f(n)\le c\cdot g(n)\}$
  • Asymptotická horní mez funkce $g(n)$ je množina funkcí $f(n)$, takových, že existuje přirozené číslo $c>0$ a existuje přirozené číslo $n_0$ tak, že pro každé $n\ge n_0$ platí $0\le f(n)\le c\cdot g(n)$
  • 

• $\Omega (g)$ … Asymptotická dolní mez

  • $\Omega (g(n))=\{f(n)\mid (\exists c\in \mathbb{N})(\exists n_0\in \mathbb{N})(\forall n\ge n_0):0\le c\cdot g(n)\le f(n)\}$
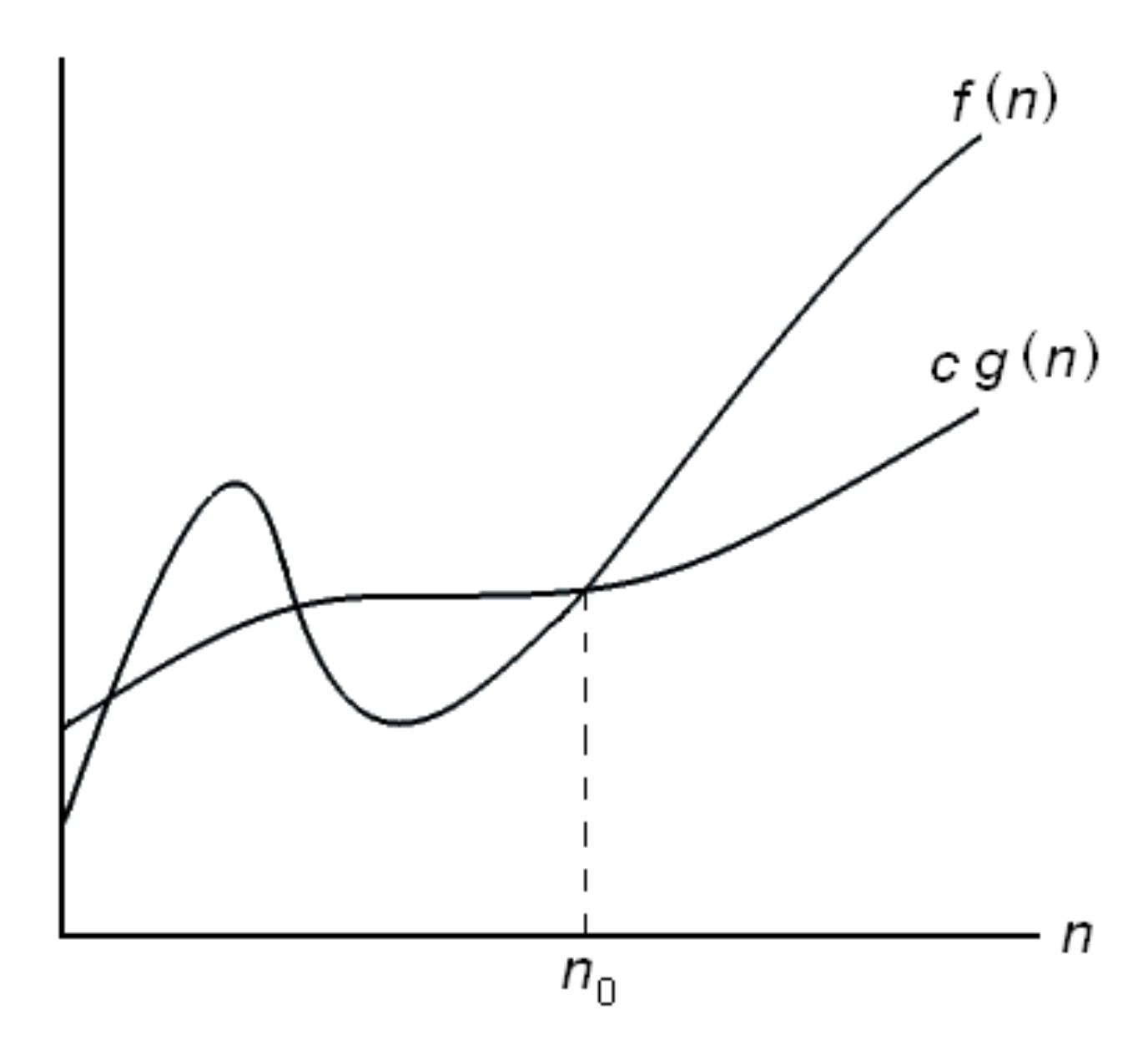
  • Asymptotická dolní mez funkce $g(n)$ je množina funkcí $f(n)$, takových že existuje přirození číslo $c>0$ a existuje přirozené číslo $n_0$ tak, že pro každé $n\ge n_0$ platí: $0\le c\cdot g(n)\le f(n)$
  • 

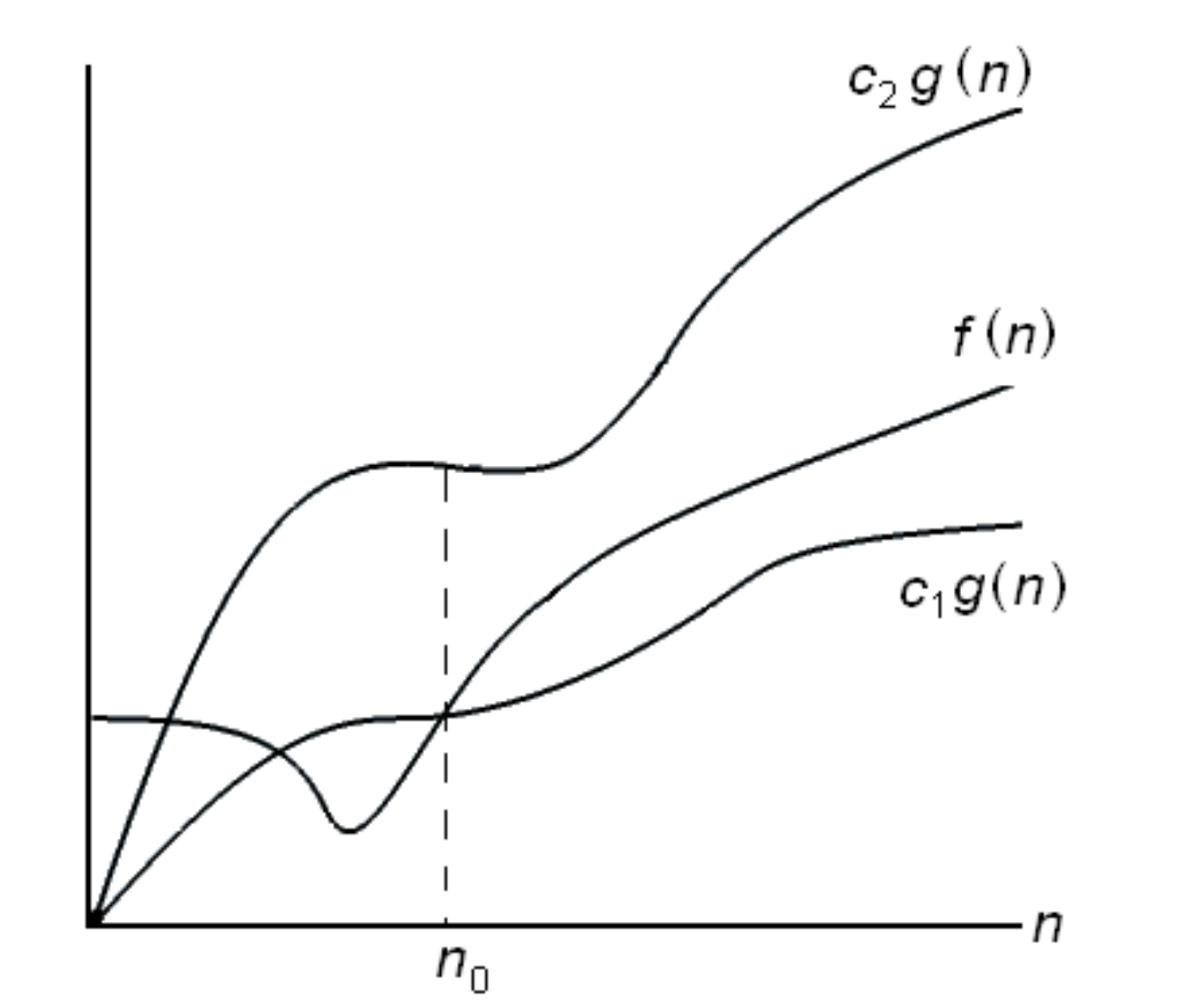
• $\theta (g)$ … Asymptotická oboustranná mez

  • popisuje těsnější popis chování funkce
  • $\theta (g(n))=\{f(n)\mid (\exists c_1\in \mathbb{N})(\exists c_2\in \mathbb{N})(\exists n_0\in \mathbb{N})(\forall n\ge n_0):0\le c_1\cdot g(n)\le f(n)\le c_2\cdot g(n)\}$
  • Asymptotická oboustranná mez funkce $g(n)$ je množina funkcí $f(n$, takových, že existují přirozená čísla $c_1>0$ a $c_2>0$ a existuje přirozené číslo $n_0$ takové, že pro každé $n\ge n_0$ platí: $0\le c_1\cdot g(n)\le f(n)\le c_2\cdot g(n)$
  • Věta: $f(n)\in \theta (g(n))$ právě když $f(n)\in O(g(n))$ a $f(n)\in \Omega (g(n))$
  • 

• $o(g)$ … Asymptotická ostrá horní mez

  • $o(g(n))=\{f(n)\mid (\forall c\in \mathbb{N})(\exists n_0\in \mathbb{N})(\forall n\ge n_0):0<f(n)<c\cdot g(n)\}$
  • Asymptotická ostrá horní mez funkce $g(n)$ je množina funkcí $f(n)$, takových, že pro každé přirozené číslo $c>0$ existuje přirozené číslo $n_0$ tak, že pro každé $n\ge n_0$ platí: $0<f(n)<c\cdot g(n)$

• $\omega (g)$ … Asymptotická ostrá dolní mez

  • $\omega (g(n))=\{f(n)\mid (\forall c\in \mathbb{N})(\exists n_0\in \mathbb{N})(\forall n\ge n_0):0<c\cdot g(n)<f(n)\}$
  • Asymptotická ostrá dolní mez funkce $g(n)$ je množina funkcí $f(n)$, takových, že pro každé přirozené číslo $c>0$ existuje přirozené číslo $n_0$ tak, že pro každé $n\ge n_0$ platí: $0<c\cdot g(n)<f(n)$

Základní pravidla (vlastnosti)

1. Ignorování konstant
   • O-notace ignoruje konstantní násobky a nízké řády členů.
   • To znamená, že $O(2n)=O(n)$ a $O(3n^2+5n)=O(n^2)$.
2. Tranzitivita
   • Pokud $f(n)=O(g(n))$ a $g(n)=O(h(n))$, pak $f(n)=O(h(n))$.
   • Umožňuje porovnávat různé algoritmy a funkce pomocí řetězení jejich asymptotických růstových charakteristik.
3. Sčítání
   • Pokud $f(n)=O(g(n))$ a $h(n)=O(p(n))$, pak $f(n)+h(n)=O(max(g(n),p(n)))$.
   • Tato vlastnost nám říká, že celkový růst funkce je ovlivněn tím, který člen domunuje při velkých hodnotách $n$.

Věta o reflexivitě odhadů

• Každá funkce je asymptoticky ekvivalentní sama sobě. Tedy pro jakoukoliv funkci $f$ platí:
  • $f=O(f)$,
  • $f=\Omega (f)$,
  • $f=\Theta (f)$.

Věta o symetrii odhadů

• $f=\Theta (g)$ právě když $g=\Theta (f)$.

Věta o symetrii horních a dolních odhadů

• $f=O(g)$ právě když $g=\Omega (f)$.
• $f=o(g)$ právě když $g=\omega (f)$.

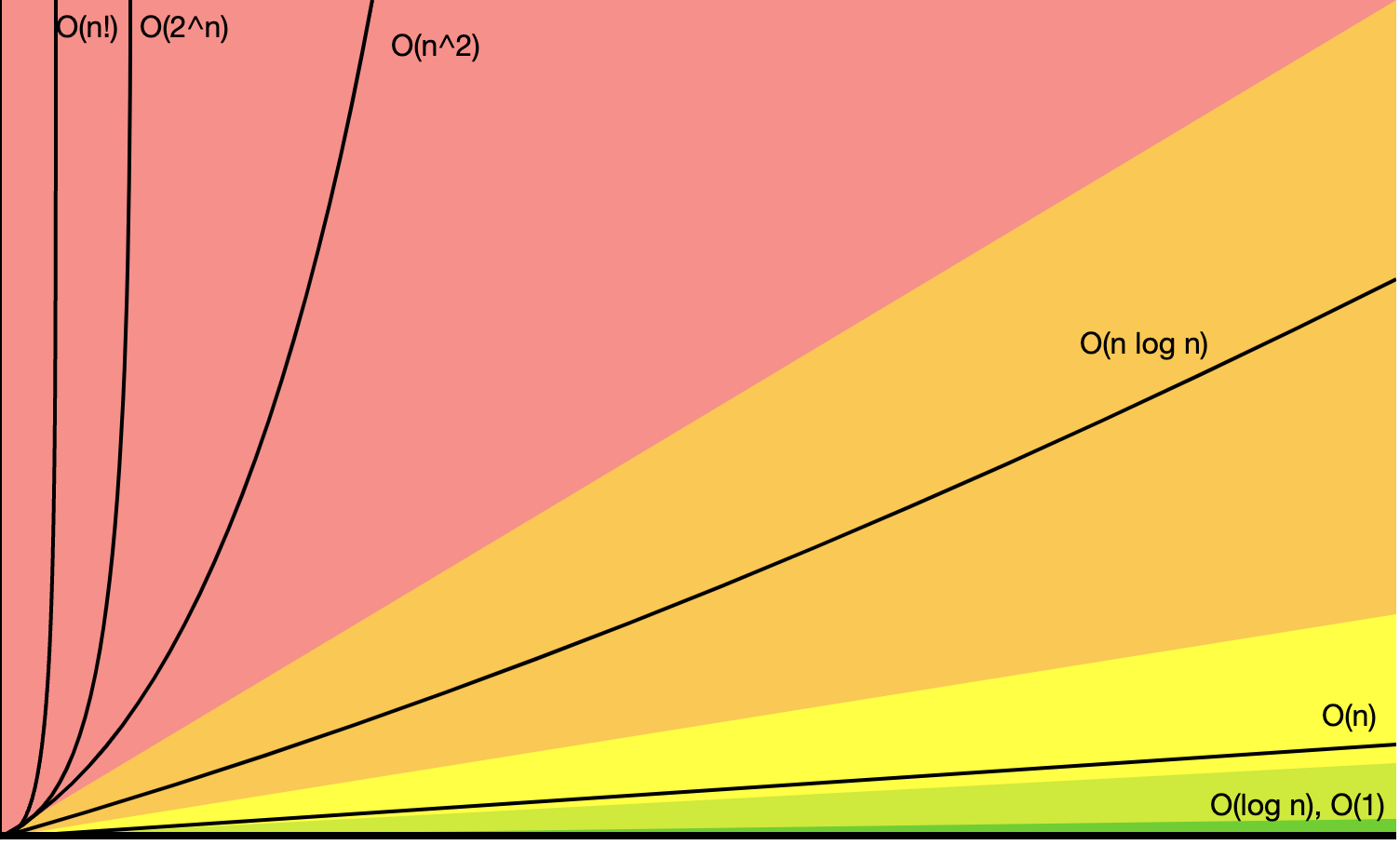
Big-O Complexity chart

Navigace

Předchozí: Algoritmus, problém, časová složitost algoritmu v nejhorším a průměrném případě Následující: Lineární datové struktury - seznam, zásobník, fronta Celý okruh: 1. Teoretické základy informačních technologií