Deterministický konečný automat
Definice
- Deterministický konečný automat je uspořádaná pětice , kde:
- je neprázdná konečná množina stavů
- je konečná množina vstupních symbolů, nazývaná také vstupní abeceda
- je přechodová funkce ve stavu
- je počáteční stav
- je množina koncových/akceptujících stavů
-
Takto definovaný automat je deterministický, protože se v každém kroku výpočtu nachází právě v jednom stavu
-
Abychom mohli definovat jazyk přijímaný daným DFA M, zavedeme rozšířenou přechodovou funkci , definovanou induktivně vzhledem k délce slova ze :
- , pro každý stav
-
Jazyk přijímaný DFA M, označovaný , je tvořen právě všemi takovými slovy, pod kterými automat přejde z počátečního stavu do některého z koncových stavů:
-
Jazyk, který je rozpoznatelný DFA, nazveme regulární
Příklad DFA M a jeho další možné reprezentace
- Nechť je , kde Pak .
- Automat M je možné reprezentovat pomocí tabulky přechodové funkce:

- Stavy automatu jsou vypsány v záhlaví řádků, vstupní symboly v záhlaví sloupců, přechodová funkce je určena obsahem vnitřních polí tabulky, počáteční stav je označen znakem a koncové stavy znakem .
- Ještě přehlednější(a proto nejčastěji používaná) je reprezentace pomocí přechodového grafu, který pro automat vypadá takto:
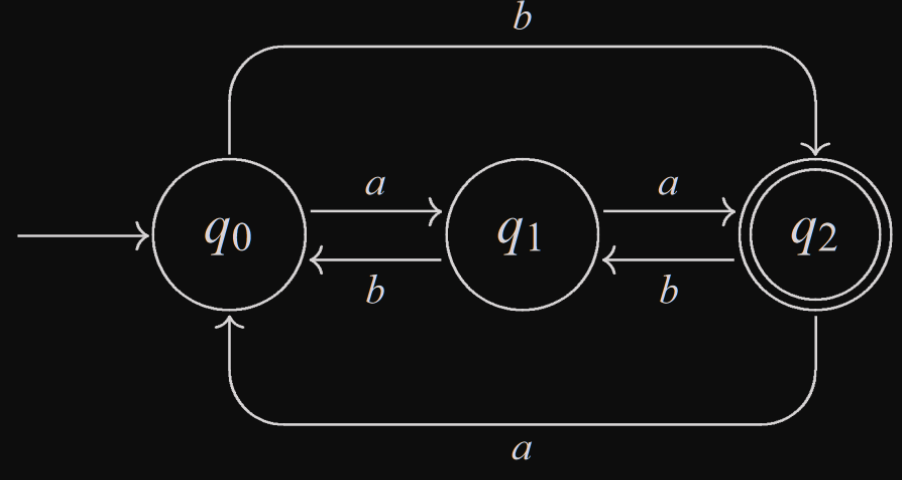
- Stavy odpovídají uzlům, přechodová funkce je znázorněna ohodnocenými hranami, vstupní abeceda je tvořena symboly, kterými jsou hrany ohodnoceny, počáteční stav je označen šipkou a koncové stavy jsou dvojitě zakroužkovány
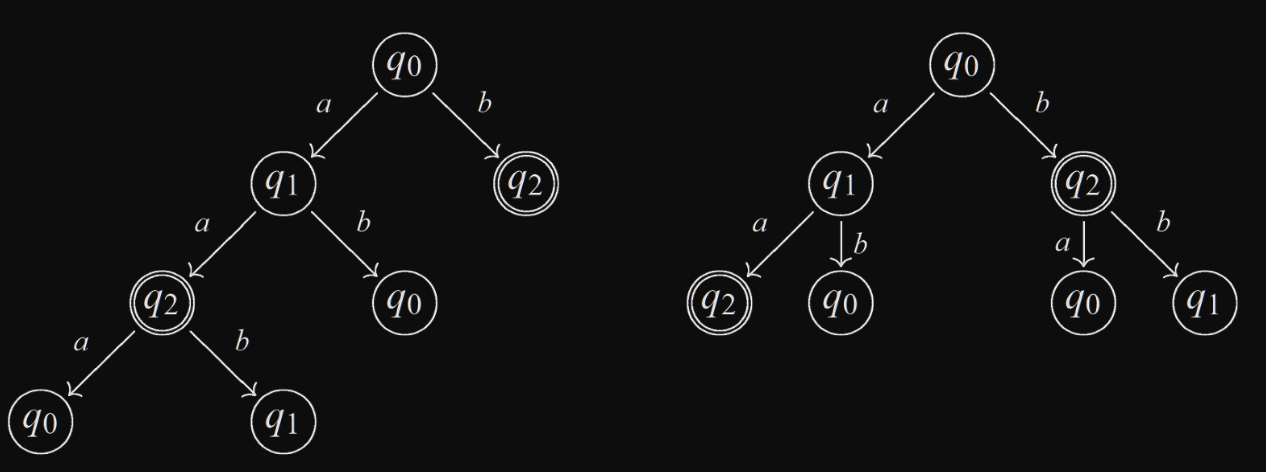
- Nakonec ještě zmiňme reprezentaci výpočetním stromem. Kočen stromu odpovídá počátečnímu stavu. Z každého uzlu, který není listem vychází právě tolik hran ohodnocených symboly vstupní abecedy, kolik má odpovídající stav následníků (je-li tedy totální, pak právě tolik hran, kolik symbolů má vstupní abeceda). Jestliže nějaký stav odpovídá více uzlům, pak hrany vycházejí jen z jednoho z těchto uzlů.
- Výpočetním stromem lze reprezentovat jen ty automaty, kde každý stav je tzv. dosažitelný z počátečního stavu
- Výpočetní strom pro daný automat není určen jednoznačně - může se lišit dle toho, zda jej konstruujeme způsobem, který odpovídá například procházení do hloubky, nebo do šířky, či dalšími možnostmi.
Konstrukce konečných automatů
- Základním trikem, který dokáže zjednodušit návrh konečného automatu, je zavedení jisté pomocní struktury na stavech. Informaci, která je spojená s daným stavem, je účelné zachytit v jeho označení.
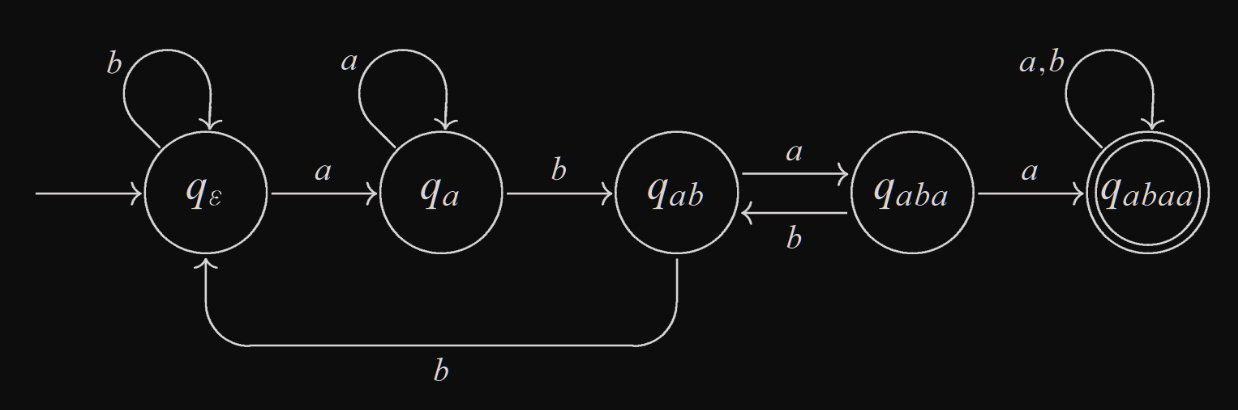
Příklad
- Máme za úkol sestrojit automat rozpoznávající jazyk
Konečný nedeterministický automat
- Jediný rozdíl je v tom, že nedeterministický automat nemusí mít pro daný stav a vstupní symbol určen následující stav jednoznačně. Slovo bude akceptování, pokud alespoň jeden z možných výpočtů nad slovem skončí v koncovém stavu.
Definice
- Nedeterministický konečný automat je uspořádaná pětice
- je neprázdná konečná množina stavů
- je konečná množina vstupních symbolů, nazývaná také vstupní abeceda
- je přechodová funkce ve tvaru
- je počáteční stav
- je množina koncových/akceptujících stavů
- Abychom mohli definovat jazyk přijímaný daným NFA M, zavedeme rozšířenou přechodovou funkci , definovanou induktivně vzhledem k délce slova ze :
- , pro každý stav
- Jazyk přijímaný NFA M je definován takto:
- Nedeterminismus je velmi silná popisný aparát, který často umožňuje zachytit strukturu jazyka elegantním a přirozeným způsobem.
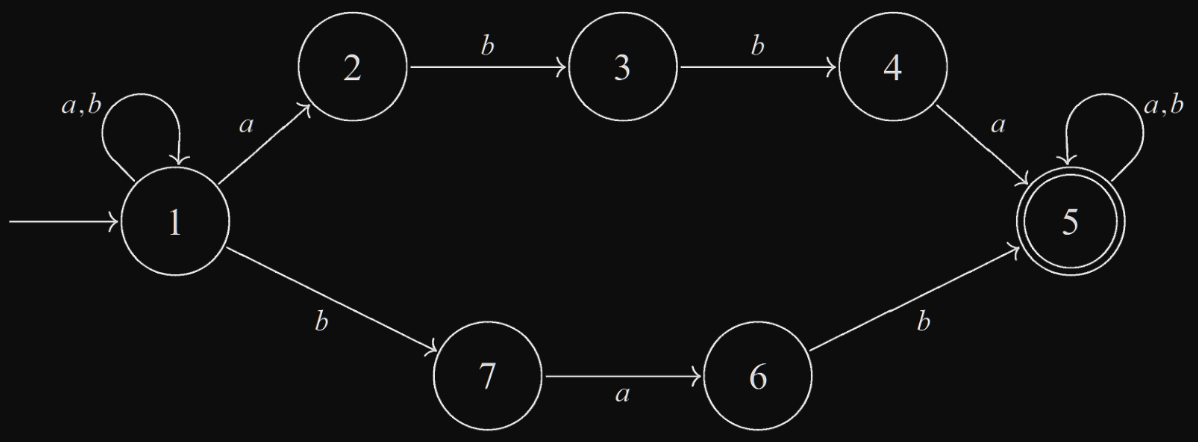
Příklad
- Navrhnout DFA, který rozpoznává , není zcela triviální.
- Naopak nederministický automat lze zkonstruovat snadno
- Nedeterminismus lze dobře využít jako popisný prostředek, nemá však vliv na výpočetní sílu konečných automatů. Ke každému nedeterministickému konečnému automatu totiž ve skutečnosti existuje ekvivalentní deterministický automat, který lze dokonce algoritmicky zkonstruovat.
Navigace
Předchozí: Regulární jazyky (definice, uzávěrové vlastnosti) Následující: Regulární výrazy, automaty s e-přechody Celý okruh: 1. Teoretické základy informatiky