Reprezentace čísel a znaků v počítači

Kódování dat

• V počítači se můžeme setkat s:

  • integer - celá čísla
  • float - desetinná čísla
  • char - znak
  • string - text

• Počítače používají binární systém (soustavu založenou na 0 a 1) pro reprezentaci všech typů dat.

• Kódování = zobrazení čísel a znaků na binární hodnoty

• Dekódování = zobrazení kódového slova (posloupnost 0 a 1) na původní číslo nebo znak

Endianita

= byte oder (pořadí bytů)

• slouží pro popis pořadí bytů, ve kterém jsou číselné hodnoty uloženy v počítačové paměti.

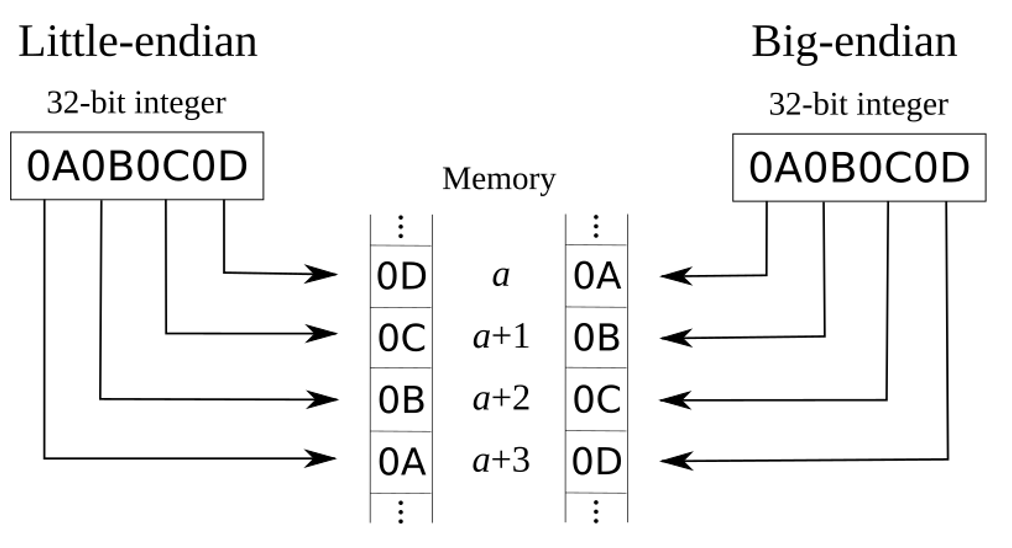
• Big-endian: nejvýznamnější byte je uložen na nejnižší adresu a další byty jsou uloženy v následujících vyšších adresách

  • často používají například síťové protokoly jako je IP

• Little-endian: nejméně významný byte je uložen na nejnižší adresu a další byty jsou uloženy v následujících vyšších adresách

  • často používán v osobních počítačích s procesory Intel a AMD využívající platformu x86

• Mixed-endian: mohou používat kombinaci předchozích

  • využíván na platformě ARM

Celá čísla

= interval ⟨min. záporné, max. kladné⟩

• hranice jsou dané počtem $n$ bitů konkrétní reprezentace

• může nastat přetečení (overflow) a nebo podtečení (underflow)

• Vážený poziční kód:

  • zápis čísla ve dvojkové poziční soustavě
  • $123=(123{)}_{10}=[\mathrm{0...1111011}{]}_2$
  • $⟨0,2^n-1⟩$

• BCD (Binary Coded Decimal):

  • každá číslice decimálního čísla je reprezentována jejím vlastním čtyřbitovým binárním ekvivalentem
  • tedy: $0=0000$, $1=0001$, $2=0010$, $3=0011$, $4=0100$, … $9=1001$.
  • čísla větší než $9$ jsou reprezentována kombinací těchto čtyřbitových skupin: $245=001001000101$
  • neefektivní využití paměti, ale je dobře čitelné

• Přímý kód (Signed magnitude):

  • jeden bit (obvykle nejvýznamnější bit) určuje znaménko čísla a zbytek bitů určuje velikost (magnitudu) čísla
  • $+13$ v 8b přímém kódu: $00001101$
  • $-13$ v 8b přímém kódu: $10001101$
  • výhodou je jednoduchost a symetrické rozložení
  • nevýhodou je dvojí nulová reprezentace

• Inverzní kód:

  • metoda pro reprezentaci záporných a kladných celých čísel v binárním systému
  • záporná čísla jsou reprezentována inverzí všech bitů kladného čísla (bitová negace)
  • nejvýznamnější bit slouží jako znaménkový bit, kde 0 značí kladné číslo a 1 záporné číslo
  • $+13=00001101$
  • $-13=11110010$
  • výhodou je jednoduchost implementace a přímé operace
  • nevýhodou je dvojí nula a složitější aritmetika

• Doplňkový kód:

  • tento formát je preferován v moderních počítačových systémech kvůli jeho efektivitě v aritmetických operacích a jednoduchému způsobu, jakým zpracovává znaménka čísel
  • nejvýznamnější bit je použit jako znaménkový bit
  • záporná čísla jsou reprezentována invertováním všech bitů kladného čísla a přičtením jedničky k výsledku
  • $+13=00001101$
  • $-13=11110011$
  • výhody jsou eliminace dvojí nuly, jednoduchá aritmetika
  • nevýhody jsou rozsah (záporná čísla mají o jedno větší rozsah) a přetečení

Čísla s řádovou čárkou

• Fixní řádová čárka:
  • počet číslic před a po desetinné čárce je pevně stanoven
    • tento přístup umožňuje rychlé a předvídatelné operace, protože všechny aritmetické operace mohou být prováděny jako operace s celými čísly bez nutnosti dynamického upravování pozice desetinné čárky
  • Předpokládejme, že máme systém s fixní řádovou čárkou, kde čtyři bity jsou vyhrazeny pro celou část a čtyři bity pro desetinnou část. Číslo: $12.375=1100.0110$
  • Výhody:
    • předvídatelnost výpočtů
    • snížené nároky na hw
    • efektivita
  • Nevýhody:
    • omezený rozsah a přesnost
    • přetečení a podtečení
    • neflexibilita
• Plovoucí řádová čárka:
  • umožňuje extrémně široký rozsah hodnot
  • užitečná v aplikacích, kde docházet k extrémním rozdílům ve velikosti čísel (vědecké výpočty, grafika, zpracování signálu, …)
  • Plovoucí řádová čárka používá tři hlavní komponenty pro uložení čísla: znaménko, exponent a mantisa
    • znaménko - určuje, zda je číslo kladné nebo záporné
    • exponent - Určuje stupně škálování mantisy. Exponent je obvykle uložen ve formátu s pevným posunem (offset), což znamená, že k jeho hodnotě je přičtena určitá konstanta (nejčastěji 127 pro jednoduchou přesnost a 1023 pro dvojitou přesnost), aby bylo možné reprezentovat záporné i kladné exponenty.
    • mantisa - vlastní číselná hodnota čísla
  • Číslo $-6.25$ by mohlo být reprezentováno jako:
    • Znaménko: $1$ (pro záporné číslo)
    • Exponent: $10000011$($130$ v decimálním systému, odpovídá reálnému exponentu $3$, protože $130-127=3$)
    • Mantisa: $10010000000000000000000$ (frakce za 1., v tomto případě 1.1001 v binární formě, což odpovídá 1.5625)
  • Výhody:
    • široký rozsah hodnot
    • flexibilita
  • Nevýhody:
    • složitost
    • přesnost
    • nestabilita

Text

= posloupnost tisknutelných znaků (písmena různých abeced, cifer a symbolů)

• + řídící znaky

• kódování znaků na binární hodnoty pomocí kódových tabulek:

• ASCII:

  • standardní kódová tabulka pro anglické abecedy a cifry
  • původně do $7$b = $128$ znaků

• Unicode:

  • rozsáhlý znakový standard, který byl vyvinut s cílem poskytnout jednotný a univerzální způsob reprezentace a manipulace s textem

• UTF:

  • kódování kódových bodů do binární reprezentace
  • různé verze: UTF-8, UTF-16

• Kód pro nový řádek - v různých systémech se používá jinak

  • LF (Line Feed) - v unixech
  • CR (Carriage Return) - starší MacOS
  • CR + LF - dos, windows

Navigace

Předchozí: Binární logika, logické operace a jejich vlastnosti, funkce a jejich úpravy, logické obvody Následující: Detekční a samoopravné kódy Celý okruh: 2. Informační technologie