- Motivate: udržovat výšku s prvky omezenou na tak, aby složitost operací (závisela lineárně na výšce stromu) zůstala .
- Jeden z přístupů vymysleli G. M. Adelson-Velskij a J. M. Landis v roce 1962 AVL stromy
-
Hlavní idea:
- Definujeme vyváženost uzlu jako rozdíl výšky levého podstromu a výšky pravého podstromu tohoto uzlu.
- Strom je přípustný (vyvážený) pokud pro každý uzel ve stromu platí, že jeho vyváženost je nebo .
-
Věta: Výška přípustného stromu je seshora omezena .
Intuice důvodu:
- pokusíme se namalovat přípustný strom, který má výšku tak, aby obsahoval co nejméně uzlů
- tím bude funkce popisující výšku stromu v závislosti na počtu uzlů “nejvíce rostoucí” a najdeme tak vztah k Fibonacciho posloupnosti.
Příklad - Úvod a vyhledávání
Operace s AVL stromy
- Operace
insertadeleteděláme jako u binárního vyhledávacího stromu. Problém ovšem je, že tyto operace mohou strom učinit nepřípustným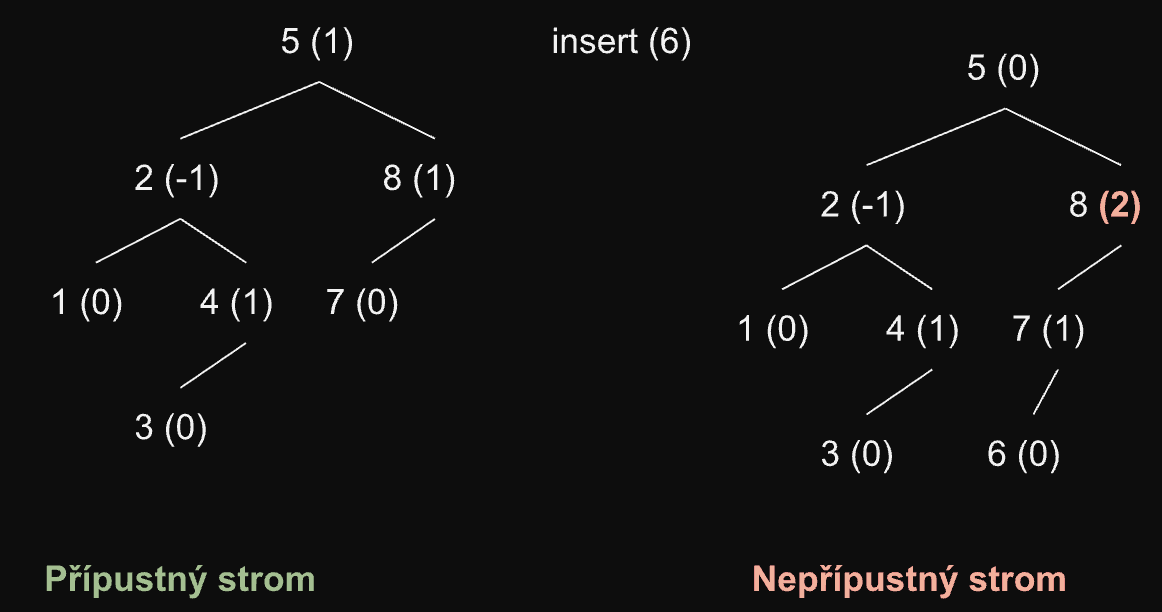
Tip
Pozorujme, že přidáním nebo odebráním uzlu můžeme změnit vyváženost pouze uzlů na cestě od přidaného/smazaného uzlu ke kořeni. Je to proto, že pro ostatní uzly se výška jejich podstromu nezmění.
- Drobnost k implementaci:
- Do uzlu přidáme položku
bf, ve které budeme udržovat vyváženost uzlu. - Po změně ve stromu procházíme strom směrem od místa změny ke kořeni.
- Změní-li se výška některého podstromu uzlu, upravíme položku
bfv tomto uzlu.
- Změní-li se výška některého podstromu uzlu, upravíme položku
- Do uzlu přidáme položku
struct node {
left, //levy potomek
right, //pravy potomek
parent, //rodic
key, //klic
bf
…
}struct tree {
root, // koren
…
}- Je-li po změně
bfrovno nebo , musíme provést některou z rotací - Procházení můžeme ukončit, pokud se výška podstromu s kořenem nezmění. Pak se totiž nezmění výšky podstromu žádného z předků uzlu , a tím se nezmění ani jejich položky
bf
Rotace
Příklad - Přidání
- existuje
- Možnosti:
- Značení:
- … výška podstromu
- … výška podstromu s kořenem
- … odvodím
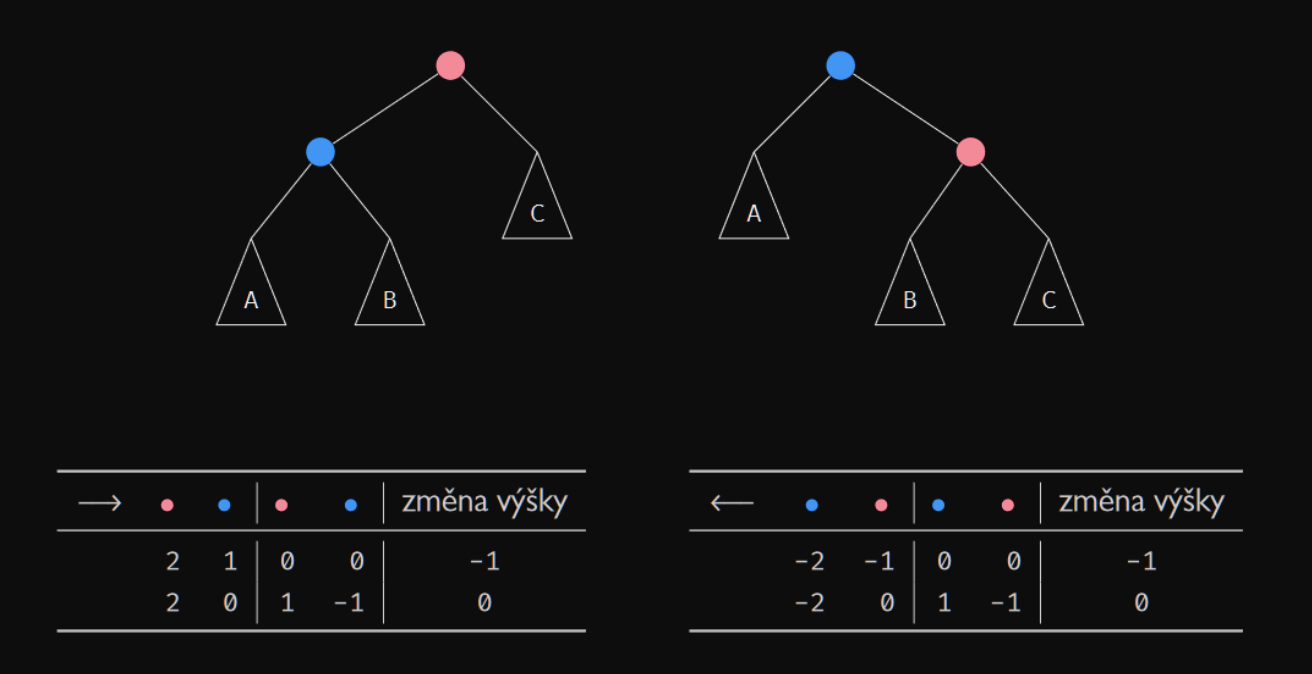
1. případ - Pravá (Levá) rotace
-
je o jedna větší než a
-
Po rotaci:
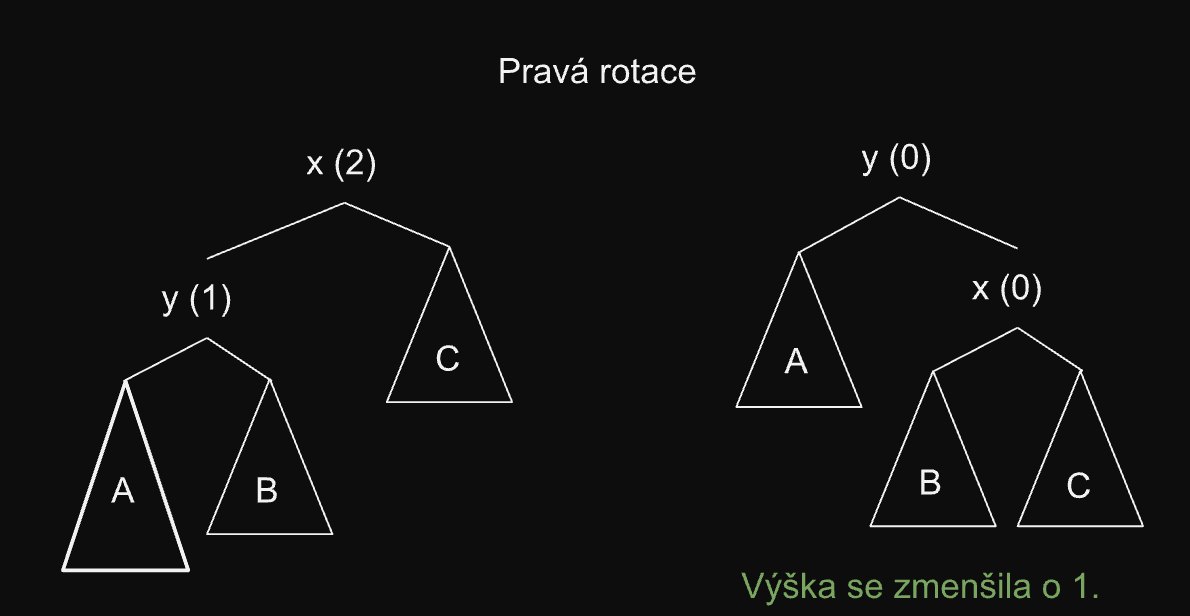
2. případ - Pravá (Levá rotace)
-
je o jedna menší než a
-
Po rotaci:
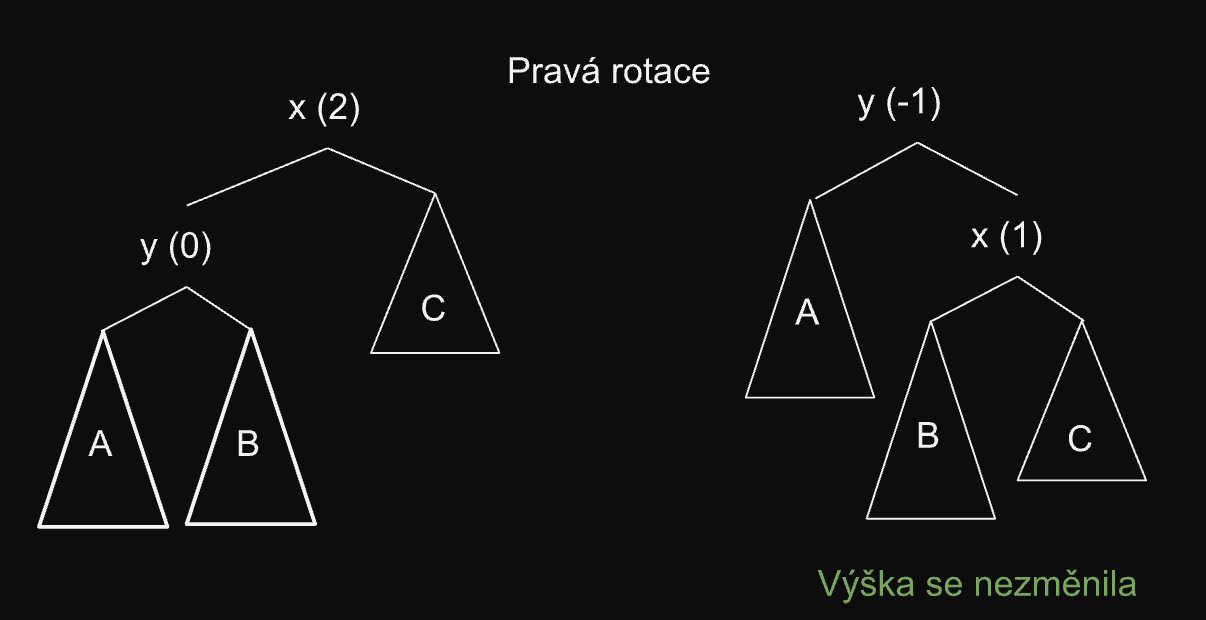
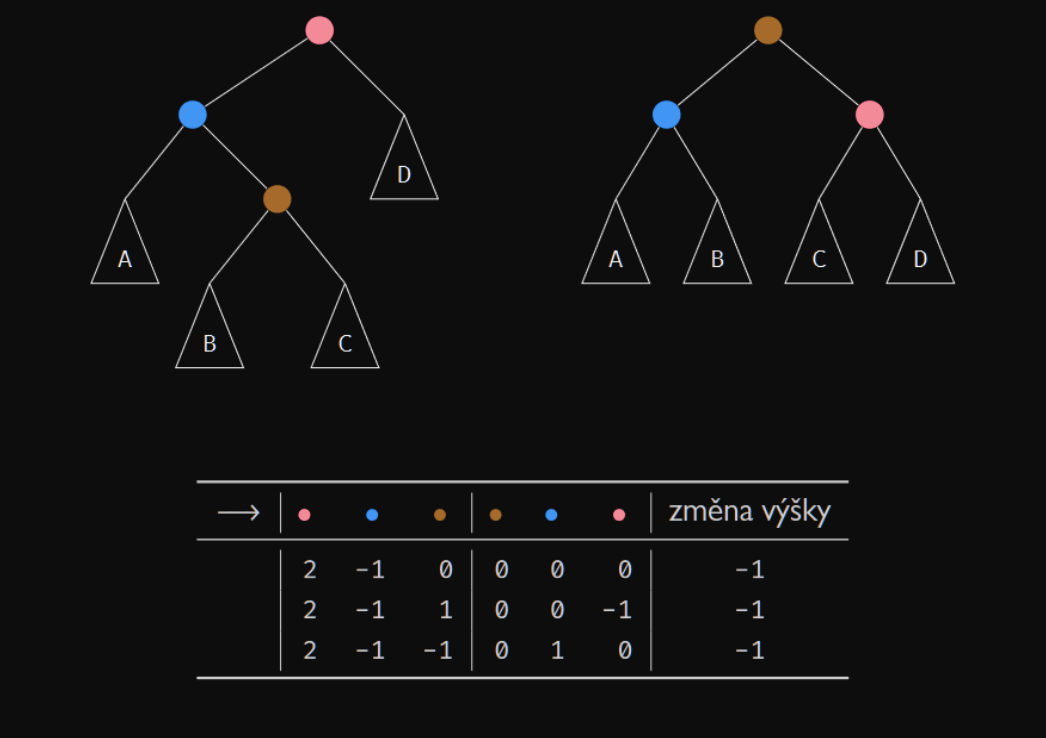
3. případ
-
je o jedna větší než a
-
Nemůžeme použít pravou rotaci, protože po přepojení je o dva větší než .
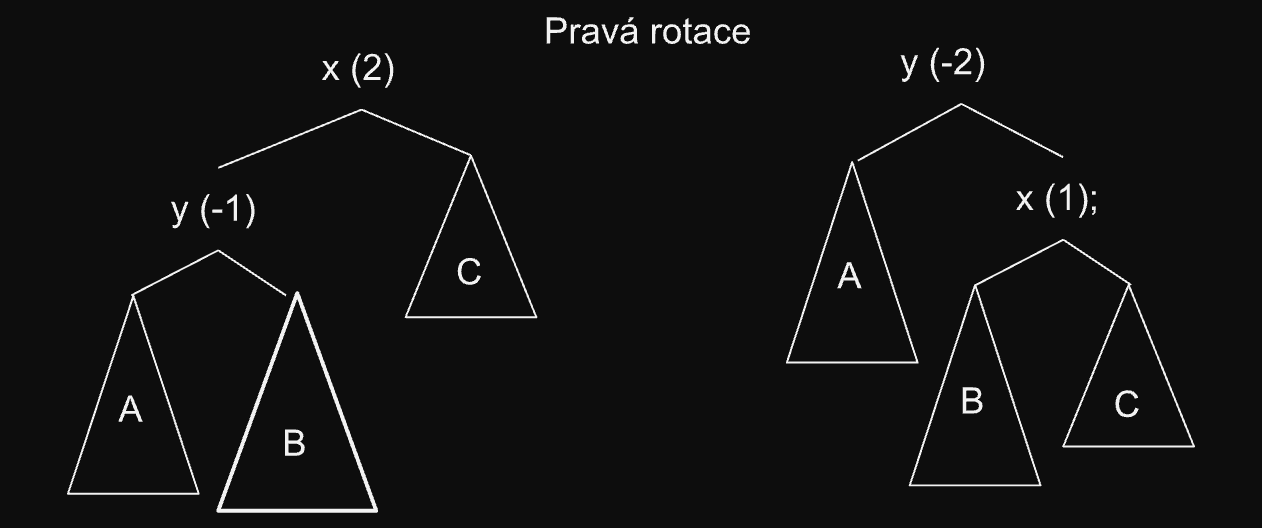
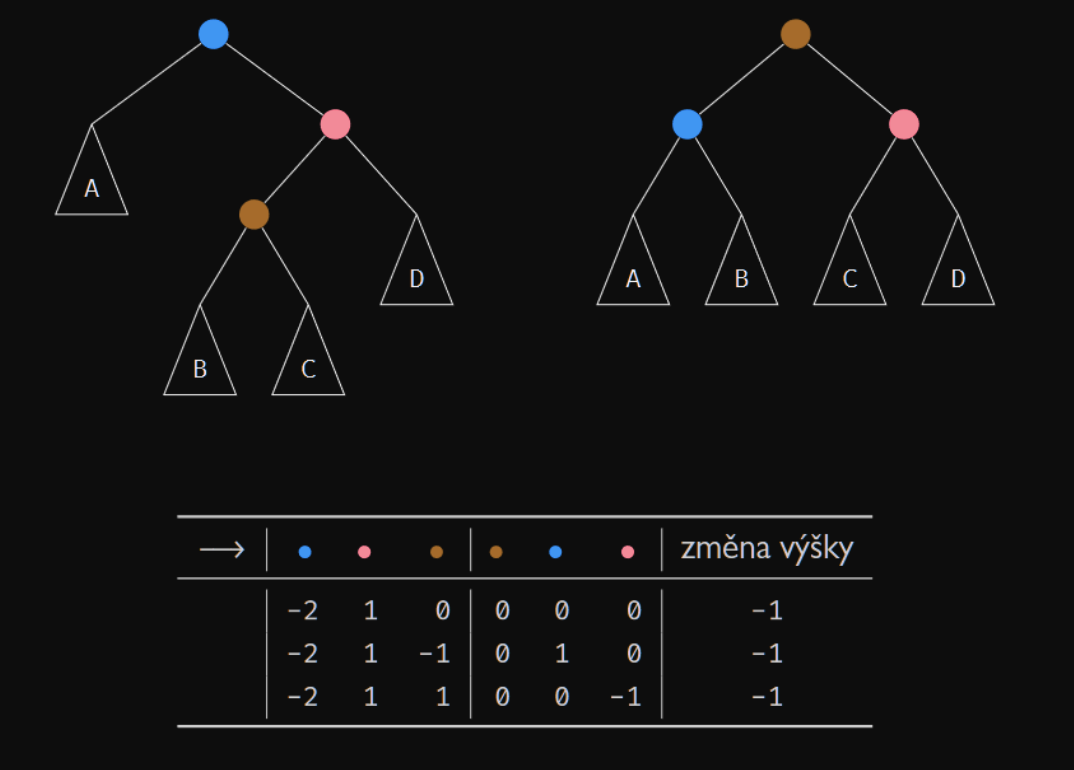
-
existuje existuje
-
je o jedna menší než a
-
Po rotaci:
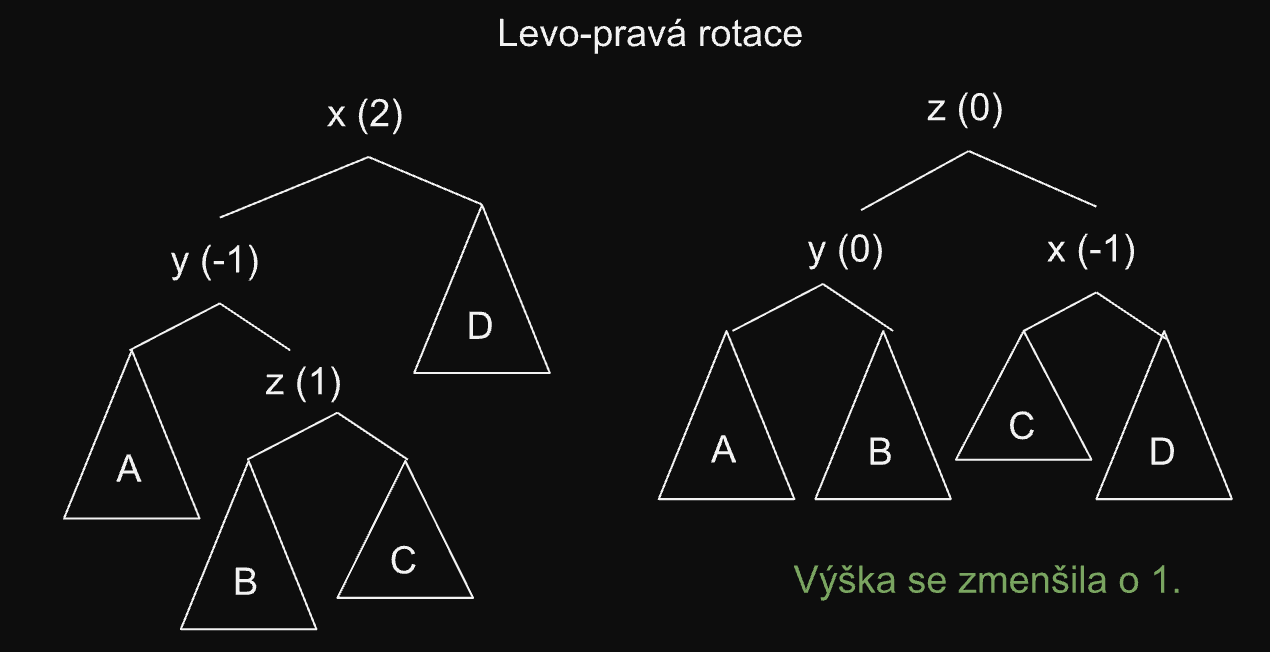
Rotace přehled
Jednoduché rotace - pravá a levá
Dvojitá rotace - levo pravá
Dvojitá rotace - pravo levá
Přidání -
- Provedeme vkládání jako v binárním vyhledávacím stromě.
- Poté jdeme po cestě od rodiče přidaného uzlu do kořene a upravujeme položky . ( je aktuální uzel, u kterého jsme provedli úpravu )
- Pokud je po úpravě rovno , algoritmus přidání končí
- Pokud je po úpravě rovno nebo , vybereme správnou rotaci, provedeme ji a algoritmus končí
- Můžeme algoritmus ukončit protože jsme museli použít rotaci, která sníží výšku stromu, který měl před rotací kořen .
- Přidáním uzlu jsme ovšem předtím výšku stromu s kořenem zvýšili o 1, rotací jsme ji pak snížili o 1, má tedy stejnou výšku jako před přidáním
- Pokud je po úpravě rovno nebo , zvýšili jsme výšku podstromu a musíme tedy pokračovat s úpravou položky u rodiče uzlu .
proc avl-insert(T, x)
tree-insert(T, x)
z = x;
u = x.p;
while u != nil
// updatujeme bf
if z == u.left then u.bf += 1
if z == u.right then u.bf -= 1
if u.bf == 0 then return // tady muzeme skoncit
if u.bf == -2 or u.bf == 2 //sníží výšku stromu
// vyber a proved správnou rotaci
return
z = u
u = u.pOdebrání -
- Provedeme odebrání jako v binárním vyhledávacím stromě.
- Poté jdeme od uzlu vybraného podle následujícího postupu ke kořeni a upravujeme položku
- Postup výběru uzlu:
- V případě, že odebíraný uzel nemá dva potomky, vybereme jeho rodiče
- V případě, že odebraný uzel má dva potomky, vybereme rodiče jeho pořádkového následníka. Pokud je tímto rodičem přímo odebáraný uzel, vybereme místo toho rodiče odebíraného uzlu
- Označme jako aktuální uzel, u kterého jsme provedli úpravu
- Pokud je po úpravě rovno nebo , vybereme správnou rotaci. Pokud rotace zmenší výšku stromu, pokračujeme k úpravě u rodiče uzlu . Jinak, pokud víme, že se nezmenšila výška podstromu s kořenem , algoritmus končí.
Příklad - mazání
Navigace
Předchozí: Binární vyhledávací stromy, operace a jejich složitosti Následující: B stromy, operace a jejich složitost Celý okruh: 1. Teoretické základy informačních technologií