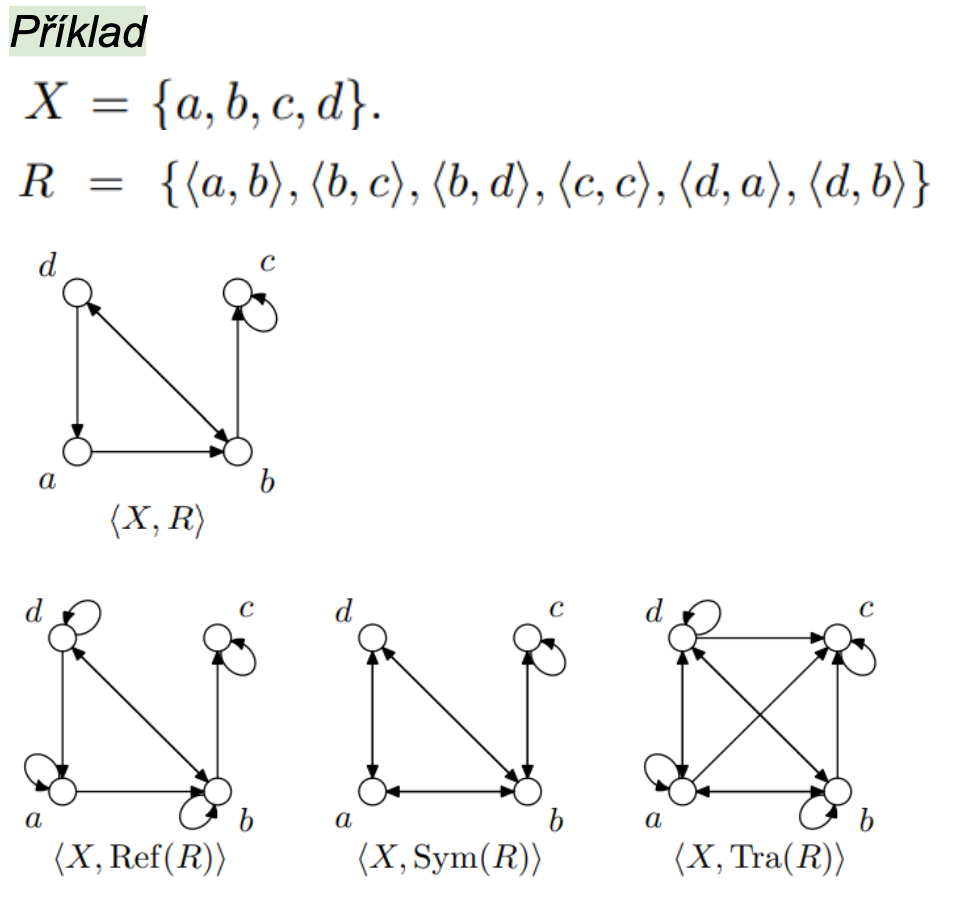
Kartézský součin
- Kartézský součin množin je množina všech uspořádaných -tic prvků z těchto množin
- Je-li , pak píšeme a říkáme -tá kartézská mocnina množiny X
- Velikost je
- Relace mezi je libovolná podmnožina kartézského součinu
Pojem relace
-
Relace je množina uspořádaných -tic prvků
-
Relace je určena:
- Aritou vztahu = číslo udávající počet objektů, které do relace vstupují
- Množiny, jejichž prvky do relace vstupují
-
Relace je matematickým protějškem pojmu vztah
-
Označuje se
-
Číslu říkáme arita relace , se nazývá -ární (unární, binární, ternární, …)
-
, právě když a
Vztah a operace s relacemi
-
Relace jsou speciální množiny (relace je podmmožina kartézského součinu) lze s nimi provádět množinové operace a vztahy
-
Rovnost (vztah)
- Označujeme symbolem ""
- Pro každé platí: , právě když
- Dvě množiny obsahují stejné prvky
- Když říkáme, že množina A se rovná množině B
- platí, právě když platí zároveň a
-
Inkluze (vztah)
- Označujeme symbolem ""
- Pro každé platí: jestliže , pak
- Všechny prvky množiny jsou také prvky množiny
- Když říkáme, že množna je podmnožinou množiny
-
Průnik (operace)
- Označujeme symbolem ""
- a
- Prvek patří do , právě když patří do A a zároveň do B
- Společné prvky
- Množiny a se nazývají navzájem disjunktní, právě když
-
Sjednocení (operace)
- Označujeme symbolem ""
- nebo
- Prvek patří do , právě když patří do A nebo do B
- Spojení všech prvků v množinách
-
Rozdíl (operace)
- Označujeme symbolem ""
- a
- Prvek patří do , právě když patří do , ale nepatří do
- Označujeme symbolem ""
-
Inverze (operace)
- Inverzní relací k relaci je relace
- “Pořadí v relaci se převrátí”
- Inverzní relací k relaci je relace
-
Skládání (operace)
- Je-li a , pak složením relací je relace
- existuje a
- “Přes společný prvek (tzv. prostředníka) spojím relace do jedné”
- Je-li a , pak složením relací je relace
Binární relace a jejich reprezentace
-
Základní způsoby reprezentace binárních relací je:
- Maticí, Grafem, Seznamem seznamů
-
Reprezentace maticí (tabulkou)
- Máme relaci , kde a . Relaci R repzentujeme maticí/tabulkou, ve které se na místě odpovídající řádku a sloupci nachází hodnota, která určuje, zda dvojici , nebo
- se nazývá matice relace
- Výhodou je přehlednost, nevýhodou je paměťová náročnost
Pro relaci
R = \set{<a,1>,<a,2>,<a,4>,<b,2>,<b,4>,<c,1>}
-
Reprezentace orientovaným grafem
- Graf binární relace dostaneme tak, že:
- Každý prvek znázorníme v rovině jako kroužek s označením daného prvku
- Pokud , nakreslíme z kroužku odpovídajícího do kroužku odpovídajícího orientovanou čáru s šipkou.
Pro relaci
R=\set{<a,b>,<a,d>,<b,d>,<c,a>}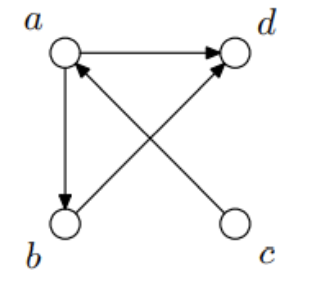
- Graf binární relace dostaneme tak, že:
-
Reprezentace seznamem seznamů
- Je vhodný pro uložení binární relace na množině
- Reprezentaci tvoří hlavní (spojový) seznam, ve kterém jsou uloženy všechny prvky množiny .
- Z každého prvku hlavního seznamu vede seznam obsahující právě ty , pro každé
- Reprezentace seznamem seznamů je paměťové úsporná a je vhodná pro počítačové zpracování
Pro relaci
R=\set{<a,b>,<a,d>,<b,d>,<c,a>}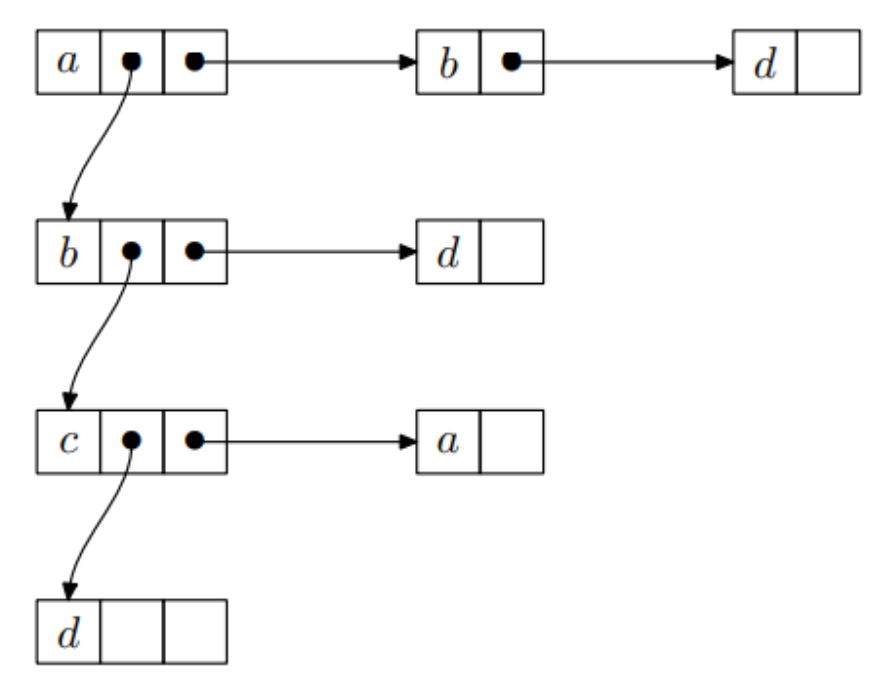
Mocnina relace
-
-tou mocninu relace zavádíme pomocí skládání relací
-
- Obecně neplatí
-
Nechť jsou binární relace na , kde
- a
- Pokud je tranzitivní, pak pro každé
- pro každé
- Pokud je konečná a pro každé , pak pro nějaké
Uzávěry relací
- Pro binární relaci na definujeme binární relace:
- = reflexivní uzávěr relace
- K relaci přidám relaci identity
- = symetrický uzávěr relace
- K relaci přidám inverzní relaci
- = tranzitivní uzávěr relace R
- =
- Sjednocení nekonečně mnoho relací , pokud ale je R definována na konečné množině , kde , pak
- = reflexivní uzávěr relace
Příklad
Navigace
Předchozí: Množiny, množinové operace, potenční množina, kartézský součin, číselné množiny, spočetné a nespočetné množiny Následující: Funkce (zobrazení) a jejich vlastnosti Celý okruh: 1. Teoretické základy informačních technologií