Regulární výrazy
Definice
- Množina regulárních výrazů (regular expressions) nad abecedou , označovaná , je definována induktivně takto:
- a pro každé je regulární výraz nad (tzv. základní regulární výrazy)
- Jsou-li , regulární výrazy nad , jsou také a regulární výrazy nad
- Každý regulární výraz vznikne po konečném počtu aplikací kroků a
-
Základní regulární výrazy se podobají symbolům, se kterými jsme se bězně setkávali. Tučně jsou zapsány proto, že je třeba je chápat jako symboly zcela nové; tyto “dvojníky” jsme zavedli proto, abychom mohli vždy snadno rozlišit mezi syntaxí a sémantikou regulárních výrazů.
-
V regulárních výrazech se mohou vyskytovat také kulaté závorky jako metasymboly, které pomáhají vymezit rozsah operátorů. Abychom jejich použití omezili na minimum, přijmeme konvenci týkající se priority operátorů: Největší prioritu má "", pak "" a nakonec "", přičemž “nadbytečné” závorky lze vypouštět.
-
Každý regulární výraz nad abecedou popisuje (jednoznačně určuje) jazyk nad abecedou (jazyk je sémantikou regulárního výrazu ) podle těchto pravidel:
- pro každé
Příklady
- Z výše řečeného se okamžitě nahlédne fakt, že jazyk je regulární nad právě když je popsatelný nějakým regulárním výrazem nad .
- Nechť je regulární výraz. Pak existuje konečný automat rozpoznávající
- Nechť je akceptovaný nějakým (libovolným) DFA, pak je popsatelný nějakým regulárním výrazem.
Struktura převeditelnosti
Nedeterministický konečný automat s -přechody
- Model nedeterministického konečného automatu je možné dála rozšířit o tzv. -kroky. Automat pak může svůj stav za určitých okolností změnit samovolně. Tato schopnost je formálně popsána pomocí -kroků, které si lze na přechodových grafech představit jako hrany, jejichž návěštím je prázdné slovo. Přes tyto hrany může automat během výpočtu na slově měnit svůj stav bez toho, aby ze vstupu cokoliv přečetl - mezi přečtením dvou po sobě jdoucích symbolů z může provést libovolné konečné množství -přechodů
Příklad
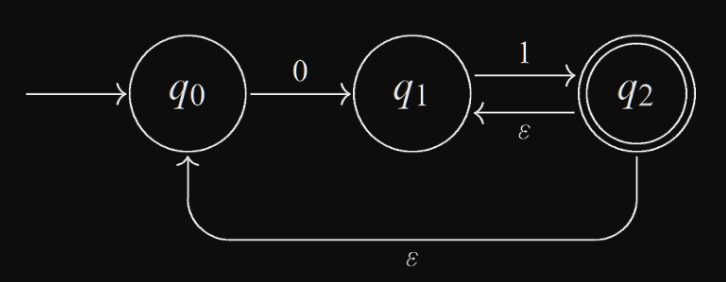
- Následující automat s -kroky rozpoznává právě ta slova , která jsou tvaru , kde a pro každé :
Definice
- Nedeterministický konečný automat s -přechody je uspořádaná pětice
- je neprázdná konečná množina stavů
- je konečná množina vstupních symbolů, nazývaná také vstupní abeceda
- je přechodová funkce ve tvaru
- je počáteční stav
- je množina koncových/akceptujících stavů
-
Rozšířenou přechodovou funkci ovšem musíme definovat odlišným způsobem. Nejprve zavedeme funkci , která pro daný stav vrací množinu stavů, kterých může dosáhnout z bez toho, aby četl vstup.
-
Pro dané je nejmenší množina taková, že platí:
- Pokud a , pak také .
-
Funkci je možné přirozeně rozšířit na množiny stavů: je-li , položíme
-
Nyní již můžeme definovat rozšířenou přechodovou funkci takto:
-
Jazyk přijímaný s -přechody je definován takto:
-
Ke každému NFA s -přechody existuje ekvivalentní NFA (bez -přechodů)
Navigace
Předchozí: Konečné automaty deterministické a nedeterministické Následující: Minimalizace konečného deterministického automatu Celý okruh: 1. Teoretické základy informatiky