Regulární jazyky (definice, uzávěrové vlastnosti)

Pojem regulární jazyk jsme používali jako pojem pro jazyk přijímaný konečným automatem a též pro pojem jazyk generovaný gramatikou typu $3$ .

Definice

Definice regulárních jazyků

Třída regulárních jazyků nad abecedou $Σ$ , označovaná jako $R (Σ)$ , je definována induktivně takto:

$\emptyset, {ϵ}$ a ${a}$ pro každé $a \in Σ$ je regulární jazyk nad $Σ$ .

Jsou-li $L_{1}, L_{2}$ regulární jazyky nad $Σ$ , jsou také $L_{1} . L_{2}, L_{1} \cup L_{2}$ a $L_{1}^{*}$ regulární jazyky nad $Σ$

Každý regulární jazyk vznikne po konečném počtu aplikací kroků $1$ a $2$ .

Jinými slovy, $R (Σ)$ je nejmenší třída jazyků nad $Σ$ splňující podmínky $1$ a $2$ .

Jazyky uvedení $a d 1$ se nazývají elementární,

operace nad jazyky uvedení $a d 2$ se nazývají regulární

Je tedy vidět, že každý regulární jazyk lze popsat určením elementárních jazyků a předpisu, který určuje jak na tyto jazyky aplikovat regulární operace.

Příklad regulárního jazyku

$L_{R} = {w \in {0, 1}^{*} ∣ w nahl \overset{ı}{ˊ} \overset{z}{ˇ} eno jako bin \overset{a}{ˊ} rn \overset{ı}{ˊ} \overset{c}{ˇ} \overset{ı}{ˊ} slo je d \overset{e}{ˇ} liteln \overset{e}{ˊ} 23}$

$23$ stavů pojmenovaných $0, 1, ..., 22$ - odpovídají $23$ zbytkům po dělení $23$

počáteční a jediný koncový stav je $0$

Příklad neregulárního jazyku

$L_{NR} = {0^{n} 1^{n} ∣ n \geq 1}$

Množina řetězců sestávajících z $n$ nul následován $n$ jedničkami takový, že $n$ je alespoň jedna

Uzávěrové vlastnosti regulárních jazyků

Uzávěrová vlastnost je tvrzení, že daná operace na jazycích, pokud je aplikovaná na jazyky z nějaké třídy (v tomto případě regulární jazyky), dává jako výsledek jazyk z této stejné třídy

Příklad použití uzávěrových vlastností

Dá se snadno ukázat, že jazyk $L_{1} = {0^{n} 1^{n} ∣ n \geq 0}$ není regulární.

$L_{2} =$ množina všech řetězců se stejným počtem $0$ a $1$ také není regulární, to je ale tězší dokázat.

Regulární jazyky jsou však uzavřeny na $\cap$ . Proto pokud by byl $L_{2}$ regulární, pak $L_{2} \cap L (0^{*} 1^{*}) = L_{1}$ , tj. $L_{1}$ by byl též regulární, ten ale není, tedy ani $L_{2}$ být nemůže.

Součinový DFA

K dokázání uzávěrových vlastností regulárního jazyka, je možné využít tzv. Součinový DFA
Součinový DFA simuluje běh více DFA zároveň
Máme dva DFA $A_{1} = (Q_{1}, Σ, δ_{1}, q_{0, 1}, F_{1})$ a $A_{2} = (Q_{2}, Σ, δ_{2}, q_{0, 2}, F_{2})$ vytvoříme DFA jako $A_{1} \times A_{2} = (Q_{1} \times Q_{2}, Σ, δ^{'}, < q_{0, 1}, q_{0, 2} >, F^{'})$ kde
- množina stavů obsahuje všechny dvojice stavů $< q_{1}, q_{2} >$ , kde $q_{1} \in Q_{1}$ a $q_{2} \in Q_{2}$
- abeceda zůstává stejná (oba automaty musí mít stejnou abecedu)
- $δ^{'} (< q_{1}, q_{2} >, a) =< δ_{1} (q_{1}, a), δ_{2} (q_{2}, a) >$ pro všechna $a \in Σ$
- počáteční stav $< q_{0, 1}, q_{0, 2} >$ je dvojice počátečních stavů z $A_{1}$ a $A_{2}$
- množina koncových stavů $F^{'}$ zvolíme podle účelu $A_{1} \times A_{2}$

Nechť $L_{1} = L (A_{1})$ a $L_{2} (A_{2})$ , pak pro ověření:
- $L_{1} = L_{2}$ zvolím $F^{'} = {< q_{1}, q_{2} >∣ (q_{1} \in F_{1} \land q_{2} \in / F_{2}) \lor (q_{1} \in / F_{1} \land q_{2} \in F_{2})}$ a pokud $L (A_{1} \times A_{2}) = \emptyset$ , pak $L_{1} = L_{2}$
- $L_{1} \subseteq L_{2}$ zvolím $F^{'} = {< q_{1}, q_{2} >∣ (q_{1} \in F_{1} \land q_{2} \in / F_{2})}$ a pokud $L (A_{1} \times A_{2}) = \emptyset$ , pak $L_{1} \subseteq L_{2}$
- $L_{1} \cap L_{2}$ zvolím $F^{'} = {< q_{1}, q_{2} >∣ (q_{1} \in F_{1} \land q_{2} \in F_{2})}$
- $L_{1} \cup L_{2}$ zvolím $F^{'} = {< q_{1}, q_{2} >∣ (q_{1} \in F_{1} \lor q_{2} \in F_{2})}$
- $L_{1} - L_{2}$ zvolím $F^{'} = {< q_{1}, q_{2} >∣ (q_{1} \in F_{1} \land q_{2} \in / F_{2})}$

Uzavřenost na sjednocení

Pokud jsou $L$ a $M$ regulurní jazyky, pak též $L \cup M$ je regulární jazyk
Důkaz: Již podle definice regulárních jazyků, nebo mohu sestrojit součinový DFA

Uzavřenost na konkatenaci

Pokud jsou $L$ a $M$ regulární jazyky, pak též $L . M$ je regulární jazyk

Důkaz

Již podle definice regulárních jazyků, nebo

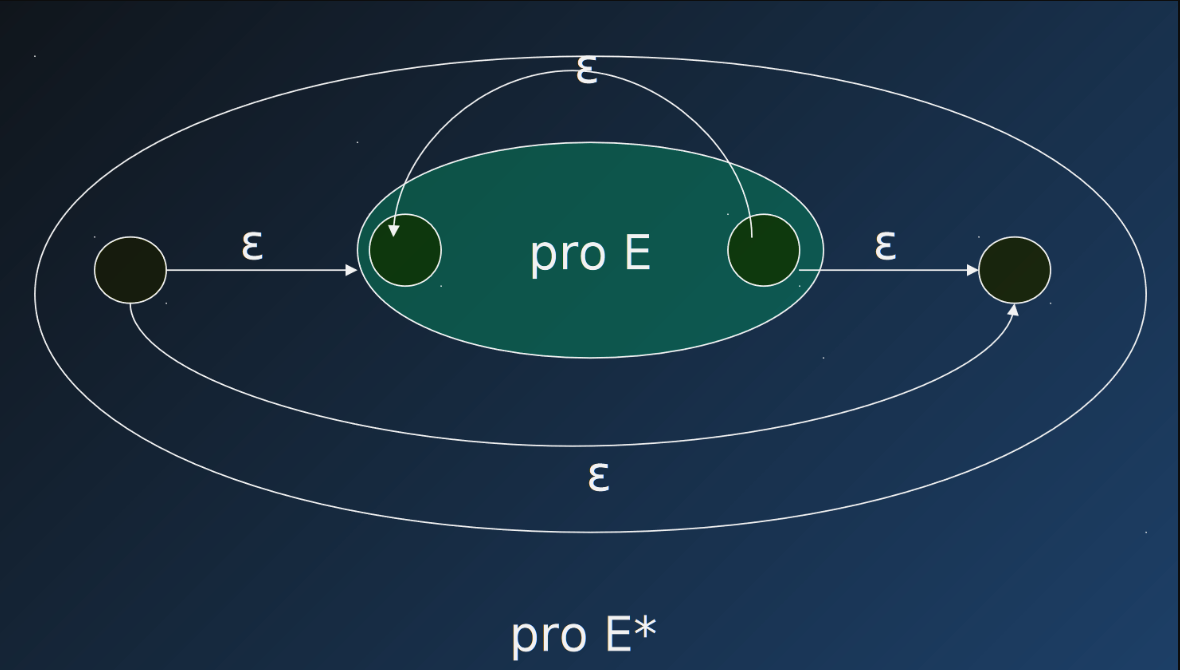
Uzavřenost na Kleeneho uzávěr

Pokud je $L$ regulární jazyk, pak též $L^{*}$ je regulární jazyk

Důkaz

Již podle definice regulárních jazyků, nebo

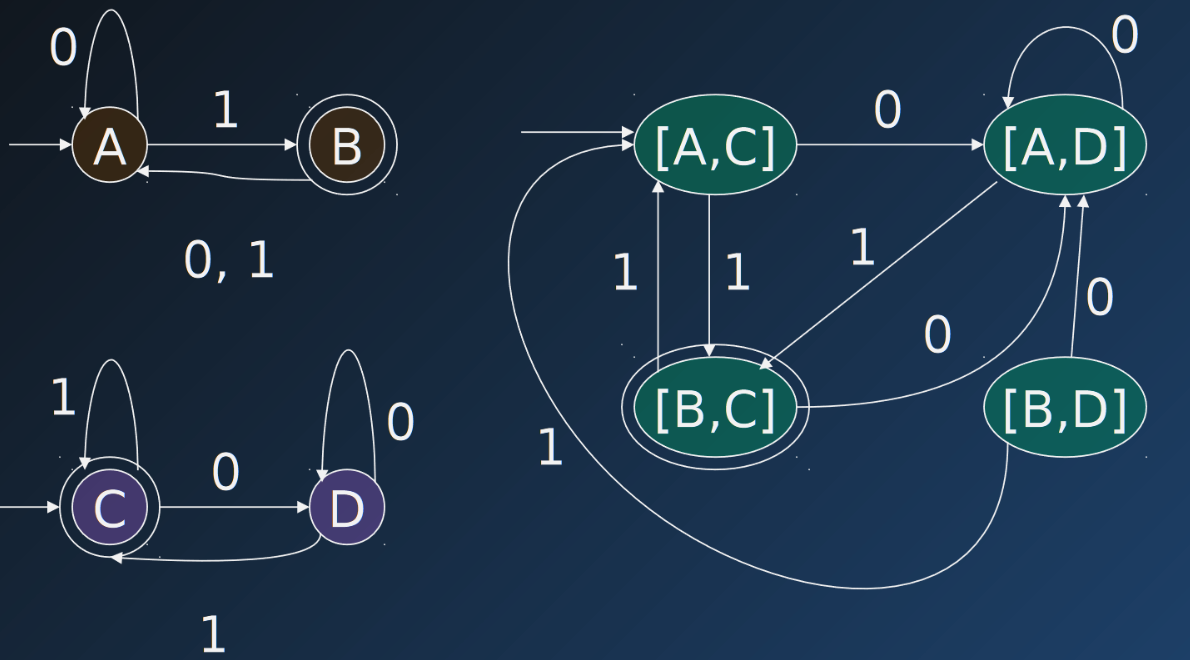
Uzavřenost na průnik

Pokud jsou $L$ a $M$ regulární jazyky, pak též $L \cap M$ je regulární jazyk

Důkaz

Mohu sestrojit součinový DFA

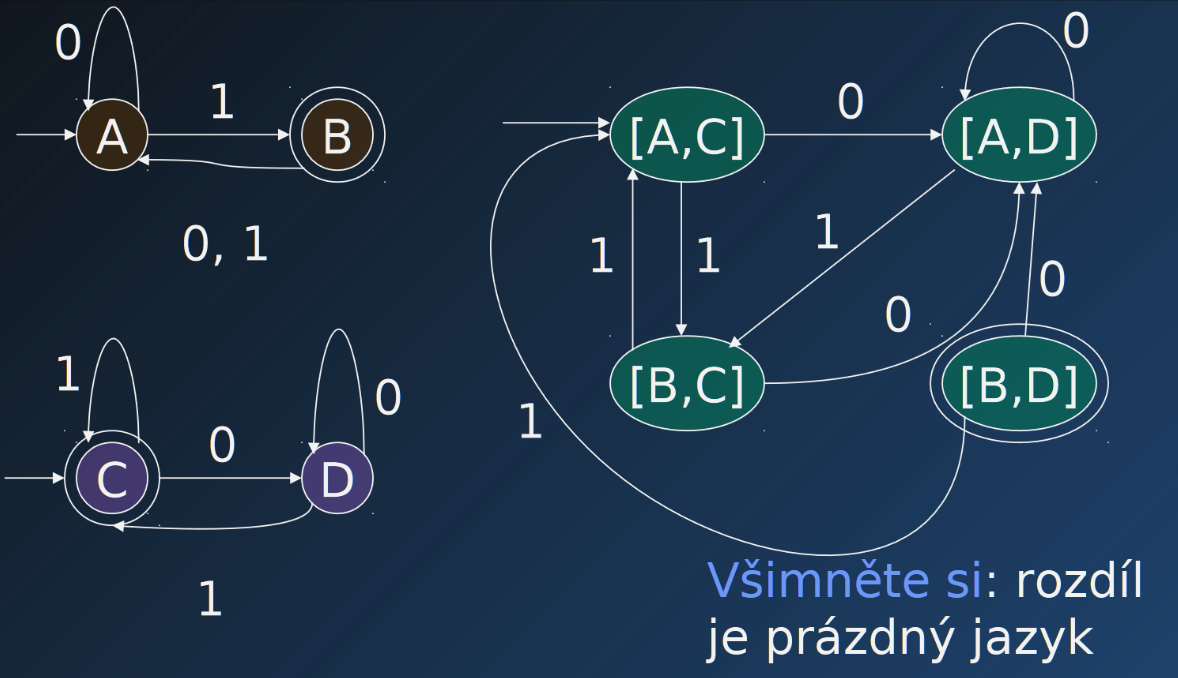
Uzavřenost na rozdíl

Pokud jsou $L$ a $M$ regulární jazyky, pak též $L - M$ je regulární jazyk

Důkaz

Mohu sestrojit součinový DFA

Uzavřenost na komplement

Pokud je $L$ regulární jazyk, pak též co- $L$ je regulární jazyk

Důkaz

Lze uvést konstruktivní důkaz:

Nechť $L$ je regulární jazyk nad abecedou $Σ$ , rozpoznávaný deterministickým konečným automatem $A = (Q, Σ, δ, q, F)$ .

Pak jazyk co- $L$ je rozpoznávaný konečným automatem co- $L = (Q, Σ, δ, q, Q - F)$

Uzavřenost na reverz

Pokud je $L$ regulární jazyk, pak též $L^{R}$ je regulární jazyk

Důkaz

Nechť $E$ je regulární výraz pro $L$ , ukážeme, jak reverzovat $E$ , čímž sestrojíme regulární výraz $E^{R}$ pro $L^{R}$

Základ: Pokud je $E$ symbol $a, ϵ,$ či $\emptyset$ , pak $E^{R} = E$

Indukce: Pokud je $E$

$F + G$ , pak $E^{R} = F^{R} + G^{R}$

$FG$ , pak $E^{R} = G^{R} F^{R}$

$F^{*}$ , pak $E^{R} = (F^{R})^{*}$

Uzavřenost na homomorfismus

Pokud je $L$ regulární jazyk a $h$ homomorfismus na jeho abecedě, pak $h (L) = {h (w) ∣ w je v L}$ je též regulární jazyk
Důkaz u inverzního homomorfismu

Uzavřenost na inverzní homomorfismus

Třída regulárních jazyků je uzavřena vůči homomorfismu a inverznímu homomorfismu
Nechť $h$ je homomorfismus a $L$ jazyk, jehož abeceda je výstupní jazyk $h$
$h^{- 1} (L) = {w ∣ h (w) le \overset{z}{ˇ} \overset{ı}{ˊ} v L}$

Důkaz

Navigace

Předchozí: Formální jazyky a jejich hierarchie Následující: Konečné automaty deterministické a nedeterministické Celý okruh: 1. Teoretické základy informatiky

Zkoušky

Explorer

Regulární jazyky (definice, uzávěrové vlastnosti)

Definice

Uzávěrové vlastnosti regulárních jazyků

Součinový DFA

Uzavřenost na sjednocení

Uzavřenost na konkatenaci

Uzavřenost na Kleeneho uzávěr

Uzavřenost na průnik

Uzavřenost na rozdíl

Uzavřenost na komplement

Uzavřenost na reverz

Uzavřenost na homomorfismus

Uzavřenost na inverzní homomorfismus

Navigace

Graph View

Table of Contents

Backlinks