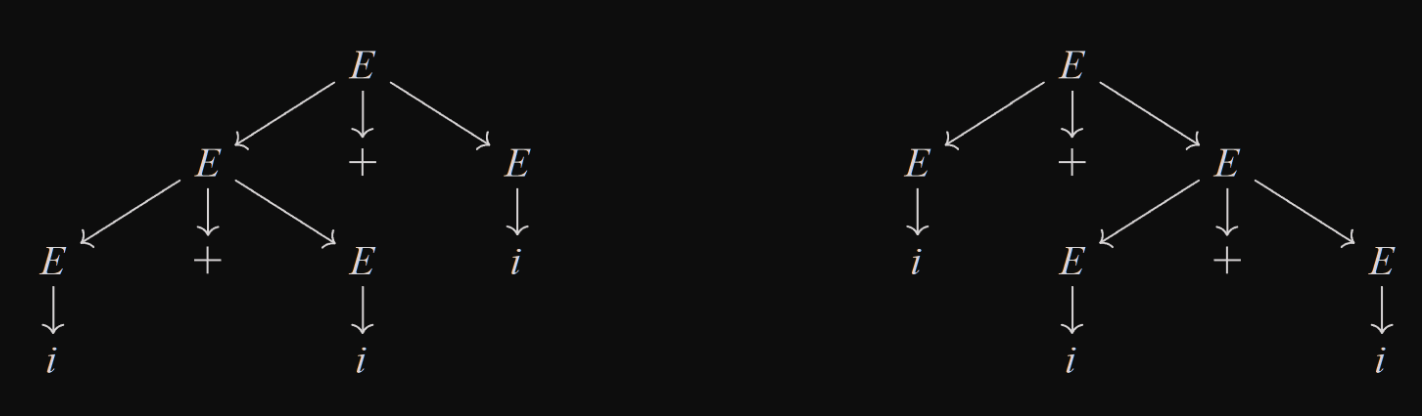Bezkontextové jazyky a jejich vlastnosti (uzávěrové vlastnosti, jednoznačnost)

• Podobně jako regulární jazyky mají též CFG i značný praktický význam, například při definici syntaxe programovacích jazyků, formalizaci pojmu syntaktická analýza a návrhu překladu programovacích jazyků a dalších.

Bezkontextová gramatika

Definice bezkontextové gramatiky

• Gramatika $G=(N,\Sigma ,P,S)$ je bezkontextová (zkratka CFG z context-free grammar), pokud jsou všechna pravidla ve tvaru $A\to \alpha$, kde $\alpha \in (\Sigma \cup N{)}^{\ast }$, tedy neterminál generuje libovolný řetězec terminálů a neterminálů

Derivační stromy

• Derivační strom je grafická reprezentace derivace nějakého řetězce v CFG

Definice derivačního stromu

• Nechť $G=(N,\Sigma ,P,S)$ je CFG. Strom $T$ nazveme derivačním stromem v $G$, právě když platí tyto podmínky:
  1. Každý uzel má návěští, které je symbolem z $N\cup \Sigma \cup \{ϵ\}$
  2. Kořen má návětší $S$
  3. Má-li vnitřní uzel návěští $A$, pak $A\in N$
  4. Má-li uzel $n$ návěští $A$ a jeho všichni synové $n_1,...,n_k$ mají v uspořádání zleva doprava návěští $X_1,...,X_k$, pak $A\to X_1,...,X_k\in P$
  5. Má-li uzel $n$ návěští $ϵ$, pak $n$ je list a je jediným synem svého otce.

• Výsledkem derivačního stromu $T$ nazveme slovo vzniklé zřetězením návěští listů v uspořádání zleva doprava.

Příklad

• Nechť $G_0$ je gramatika s pravidly

$$\begin{array}{r}E\to E+T|T\\ T\to T\ast F|F\\ F\to (E)|i\end{array}$$

pak derivační strom reprezentuje deset vzájemně ekvivalentních derivací, např.

1. $E\Rightarrow E+T\Rightarrow T+T\Rightarrow F+T\Rightarrow i+T\Rightarrow i+F\Rightarrow i+i$ nebo
2. $E\Rightarrow E+T\Rightarrow E+F\Rightarrow E+i\Rightarrow T+i\Rightarrow F+i\Rightarrow i+i$ a též
3. $E\Rightarrow E+T\Rightarrow T+T\Rightarrow T+F\Rightarrow F+F\Rightarrow F+i\Rightarrow i+i$ a další

• Všimněme si, že $1$ je levá, kdežto $2$ je pravá derivace.

• CFG $G$ je víceznačná/nejednoznačná, pokud existuje řetězec $S{\Rightarrow }^{\ast }\alpha$, který je derivací alespoň dvou různých derivačních stromů (v opačném případě je $G$ jednoznačná)
• Bezkontextový jazyk je jednoznačný, pokud existuje jednoznačná gramatika, která jej generuje (víceznačnost je vlastnost gramatiky, nikoliv jazyka který generuje)
• Pro některé bezkontextové jazyky neexistuje jednoznačná gramatika, takový jazyk je dědičně víceznačný

Příklad

• Gramatika $G_1$ s pravidly $E\to E+E|E\ast E|(E)|i$, která je ekvivalentní s gramatikou $G_0$ z příkladu výše. Je víceznačná, např. protože věta $i+i+i$ má dvě různé levé derivace a jim odpovídající dva různé derivační stromy:

• Chromského normální forma

  • Řekneme, že CFG $G=(N,\Sigma ,P,S)$ je v Chromského normální formě, právě když je $G$ bez $ϵ$-pravidel a každé pravidlo z $P$ má jeden z těchto tvarů:
    • $A\to BC,B,C\in N$
    • $A\to a,a\in \Sigma$

• Greibachová normální forma

  • Řekneme, že CFG $G=(N,\Sigma ,P,S)$ je v Greibachové normální formě, právě když je $G$ bez $ϵ$-pravidel a každé pravidlo z $P$ je tvaru $A\to a\alpha (a\in \Sigma ,\alpha \in N^{\ast })$

Bezkontextové jazyky

• Jazyk, který je definovaný nějakou bezkontextovou gramatikou

Vyjádření bezkontextových jazyků

• Nechť máme bezkontextový jazyk $L$
  1. $L=L(G)$ pro nějakou CFG $G$
     • (Lze vyjádřit pomocí bezkontextové gramatiky)
  2. $L=L(M)$ pro nějaký PDA $M$
     • (Lze vyjádřit pomocí zásobníkového automatu akceptující pomocí koncového stavu)
  3. $L=L_e(N)$ pro nějaký PDA $N$
     • (Lze vyjádřit pomocí zásobníkového automatu akceptující pomocí prázdného zásobníku)

Přehled rozhodnutelných vlastností CFL

• Řetězec $w$ patří do bezkontextového jazyka $L$.
  • Algoritmus CYK
• Bezkontextový jazyk $L$ je prázdný.
  • Umíme odstranit neterminály, které negenerují žádný terminální řetězec, jestliže je počáteční symbol jeden z nich, pak je bezkontextový jazyk prázdný; jinak ne
• Bezkontextový jazyk $L$ je nekonečný.
  • Použij konstantu $n$ z pumping lemmatu.
  • Jestliže existuje řetězec v jazyku délky mezi $n$ a $2n-1$, pak je jazyk nekončený; jinak je konečný.

Uzávěrové vlastnosti bezkontextových jazyků

• V níže uvedených důkazech lze použít jak bezkontextových gramatik, tak i zásobníkových automatů.

Uzavřenost na sjednocení, konkatenaci a Kleeneho uzávěr

• Třída všech bezkontextových jazyků je uzavřena vzhledem k operaci sjednocení, zřetězení (konkatenace), iteraci (Kleeneho uzávěr) a pozitivní iteraci

Důkaz

Neuzavřenost na průnik a doplněk

• Třída všech bezkontextových jazyků není uzavřena vzhledem k operaci průnik a doplněk.

Důkaz

Uzavřenost na homomorfismu a inverzní homomorfismus

• Třída všech bezkontextových jazyků je uzavřena vzhledem k substituci

Důkaz

• Třída všech bezkontextových jazyků je uzavřena vůči homomorfismu a izomorfismu

Důkaz

Uzavřenost na reverz

• Třída všech bezkontextových jazyků je uzavřena na reverz

Důkaz

• Nechť $L$ CFL generovaný gramatikou $G$
• Sestrojíme gramatiku pro $L^R$ tak, že otočíme pravou stranu každého pravidla
• Např. Nechť $G$ má pravidla $S\to 0S1|01$. Pak reverz jazyka $L(G)$ má gramatiku $S\to 1S0|10$

Navigace

Předchozí: Pumping lemma Následující: Zásobníkové automaty Celý okruh: 1. Teoretické základy informatiky