Limita funkce včetně nevlastních, jednostranné limity

Okolí bodu

• Nechť $a\in \mathbb{R}$ a je dáno $\delta \in \mathbb{R},\delta >0$, pak interval $U_{\delta }(a)=(a-\delta ,a+\delta )$ nazýváme $\delta$-okolím bodu $a$.
• Interval $U_{\delta }^{-}(a)=⟨a-\delta ,a)$ nazýváme levým $\delta$-okolím bodu $a$
• Interval $U_{\delta }^{+}=(a,a+\delta ⟩$ nazýváme pravým $\delta$-okolím bodu $a$

Isibalo - Okolí bodu

Prstencové okolí bodu

• Prstencovým $\delta$-okolím bodu $a$ rozumíme množinu $P_{\delta }(a)=U_{\delta }(a)\setminus \{a\}=(a-\delta ,a)\cup (a,a+\delta )$
• Levé a pravé prstencové $\delta$-okolí: $P_{\delta }^{-}=U_{\delta }^{-}\setminus \{a\}=(a-\delta ,a)$ $P_{\delta }^{+}=U_{\delta }^{+}\setminus \{a\}=(a,a+\delta )$

Okolí na rozšířené reálné ose

• Nechť je dáno číslo $k\in \mathbb{R}$. Okolím bodu $\infty$ rozumíme interval $P_k(\infty )=U_k(\infty )=(k,\infty ),$
• Okolím bodu $-\infty$ rozumíme interval $P_k(-\infty )=U_k(-\infty )=(-\infty ,k)$

Limita funkce

• Nechť $f:\mathbb{R}\to \mathbb{R}$. Říkáme, že $f$ má v bodě $a\in {\mathbb{R}}^{\ast }$ limitu $A\in {\mathbb{R}}^{\ast }$, právě když platí podmínka $\forall U(A)\exists P(a)\forall x\in \mathbb{R}:(x\in P(a)\Rightarrow f(x)\in U(A))$

• Píšeme ${\lim }_{x\to a}f(x)=A$.

• Pro $a\in \mathbb{R}$ jde o limitu ve vlastním bodě, zatímco pro $a\in \{-\infty ,\infty \}$ jde o limitu v nevlastním bodě

• Je-li $A\in \mathbb{R}$, říkáme, že $f$ má vlastní limitu, zatímco je-li $A\in \{-\infty ,\infty \}$, říkáme, že $f$ má nevlastní limitu.

Isibalo - Úvod do limity funkce

Jednostranné limity

• Často je třeba rozlišit, zda se zajímáme o hodnoty funkce $f$ v blízkosti bodu $a\in \mathbb{R}$ pro $x<a$ nebo $x>a$, je tak vhodné zavést pojem jednostranné limity
• Nechť $f:\mathbb{R}\to \mathbb{R}$. Říkáme, že $f$ má v bodě $a\in \mathbb{R}$ limitu $A\in {\mathbb{R}}^{\ast }$ zprava, právě když platí podmínka $\forall U(A)\exists P^{+}(a)\forall x\in \mathbb{R}:(x\in P^{+}(a)\Rightarrow f(x)\in U(A))$
• Píšeme ${\lim }_{x\to a^{+}}f(x)=A$
• Podobně lze popsat limitu zleva, kde píšeme $P^{-}(a)$ místo $P^{+}(a)$ a ${\lim }_{x\to a^{-}}f(x)=A$
• Funkce $f$ má v bodě $a$ limitu $A$, právě když existují obě jednostranné limity (limity zprava a zleva) a jsou si rovny
  • např. $f(x)=sgn(x)$ v bodě 0 limitu nemá, protože:
    • ${\lim }_{x\to 0^{-}}sgn(x)=-1$
    • ${\lim }_{x\to 0^{+}}sgn(x)=1$

Isibalo - Další úvahy a motivace

Isibalo - Jednostranné limity

Typy limit funkce

• Rozlišujeme $4$ typy limit podle toho, jestli $a$, $A$ nabývá reálných nebo hodnot $\pm \infty$

Isibalo - Typy limit funkce

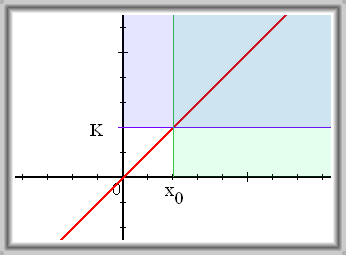
Vlastní limita ve vlastním bodě

pro $a,A\in \mathbb{R}$

• Jdeme k nějaké konkrétní hodnotě a vyjde nám konkrétní výsledek.
• např. ${\lim }_{x\to 1}(\frac{x^2-1}{x-1})=2$

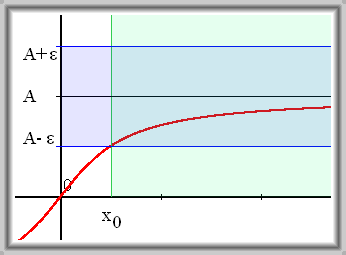
Vlastní limita v nevlastním bodě

• pro $a\in \pm \infty \wedge A\in \mathbb{R}$
• pro hodně vzdálené body $x$ se funkční hodnoty přibližují k nějaké reálné funkční hodnotě $A$
• např. ${\lim }_{x\to \infty }(\frac{x+1}{x})=1$

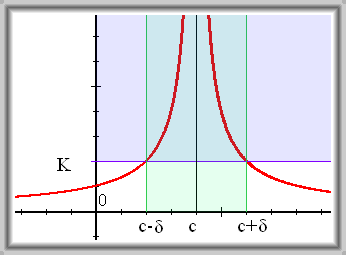
Nevlastní limita ve vlastním bodě

• pro $a\in \mathbb{R}\wedge A\in \pm \infty$
• např. ${\lim }_{x\to 0}(\frac{1}{x^2})=+\infty$

Nevlastní limita v nevlastním bodě

• pro $a,A\in \pm \infty$
• funkční hodnoty vzdálených $x$ konverguje k $\pm \infty$
• např. ${\lim }_{x\to \infty }(x+2)=\infty$

Použití limity funkce

1. Vyšetření průběhu funkcí
   • Určení asymptot: Limity umožňují nalézt asymptoty funkce
     • (přímky, ke kterým se funkce nekonečně přibližuje)
   • Chování v nekonečnu: Limity určují, jak se funkce chová, když se argument blíží k $\pm \infty$
2. Spojitost funkcí
   • Definice spojitosti
     • Funkce je spojitá v bodě, pokud se limita funkce v tomto bodě rovná funkční hodnotě v tomto bodě.
3. Derivace
   • Definice derivace
     • Derivace funkce v bodě je definována jako limita rozdílového podílu pro $h$ blížící se k nule.
   • Aplikace derivací:
     • Derivace se používají k určení rychlosti změny, nalezení maxima a minima funkcí, a v mnoha fyzikálních a technických aplikacích.
4. Integrály
   • Definice integrálu
     • limita Riemannových součtů je definována počtem dělení intervalu $n$, pro $n$ jdoucí k nekonečnu.
   • Aplikace integrálů: Integrály se používají k výpočtu obsahu plochy vymezené danými funkcemi, objemu rotačních těles, délky křivky, …

Vlastnosti limity funkce

• Zápis ${\lim }_{x\to a}f(x)=A$ znamená, že limita v bodě $a$ existuje a je rovna $A$.

1) Lokální vlastnost limity

• Nechť $f:\mathbb{R}\to \mathbb{R}$ a $g:\mathbb{R}\to \mathbb{R}$. Nechť dále existuje $P(a)$ takové, že $\forall x\in P(a)$ platí $f(x)=g(x)$. Pak ${\lim }_{x\to a}f(x)=A$, právě když ${\lim }_{x\to a}g(x)=A$.

2) O jednoznačnosti limity

• Pro $f:\mathbb{R}\to \mathbb{R}$, $a\in {\mathbb{R}}^{\ast }$ existuje nejvýše jedna limita $f$ v $a$.
  • stejně tak pro limitu zleva, resp. zprava

3) O jednostranných limitách

• Nechť $f:\mathbb{R}\to \mathbb{R}$, $a\in \mathbb{R}$. Pak ${\lim }_{x\to a}f(x)=A\in {\mathbb{R}}^{\ast }$, právě když ${\lim }_{x\to a^{+}}f(x)={\lim }_{x\to a^{-}}f(x)=A$.
  • obě jednostranné limity musí být rovny

4) O omezenosti

• Nechť $f:\mathbb{R}\to \mathbb{R}$, $a\in {\mathbb{R}}^{\ast }$ a nechť ${\lim }_{x\to a}f(x)=A\in \mathbb{R}$. Pak existuje $P(a)\subset D(f)$ takové, že $f$ je na $P(a)$ omezená.
  • to znamená, že existuje takové $K>0$ takové, že pro $x\in P(a)$ platí $|f(x)|\le K$
  • $x\in U(a)\to x\in \mathbb{R}$

5) O limitě absolutní hodnoty

• Nechť $f:\mathbb{R}\to \mathbb{R}$, $a\in {\mathbb{R}}^{\ast }$. Jestliže ${\lim }_{x\to a}f(x)=A\in {\mathbb{R}}^{\ast }$, pak ${\lim }_{x\to a}|f(x)|=|A|$.

6) O aritmetických operacích s limitami

• Nechť $f,g:\mathbb{R}\to \mathbb{R}$, $a\in {\mathbb{R}}^{\ast }$, ${\lim }_{x\to a}f(x)=A$, ${\lim }_{x\to a}g(x)=B$ a $A,B\in {\mathbb{R}}^{\ast }$. Potom:

1. Je-li součet $A+B$ definován, je ${\lim }_{x\to a}(f(x)+g(x))=A+B$
   • limita součtu je součet limit
2. Je-li součin $A\cdot B$ definován, je ${\lim }_{x\to a}(f(x)\cdot g(x))=A\cdot B$
   • limita součinu je součin limit
3. Je-li podíl $\frac{A}{B}$ definován, je ${\lim }_{x\to a}\frac{f(x)}{g(x)}=\frac{A}{B}$
   • limita podílu je podíl limit

7) O limitě složené funkce

• Nechť $f,g:\mathbb{R}\to \mathbb{R}$, $a\in {\mathbb{R}}^{\ast }$. Nechť dále současně platí podmínky:

1. ${\lim }_{x\to a}f(x)=A\in {\mathbb{R}}^{\ast }$,
2. ${\lim }_{y\to A}g(y)=B\in {\mathbb{R}}^{\ast }$,
3. existuje $P(a)$ takové, že $\forall x\in \mathbb{R}$ platí: je-li $x\in P(a)$ pak $f(x)\ne A$. - (pro $x$ dostatečně blízká k $a$, tak že $f(x)\ne A$) Pak ${\lim }_{x\to a}(g\circ f)(x)={\lim }_{x\to a}g(f(x))=B$.

8) O limitním přechodu v nerovnost

• Nechť $f,g:\mathbb{R}\to \mathbb{R}$, $a\in {\mathbb{R}}^{\ast }$. Nechť dále ${\lim }_{x\to a}f(x)=A\in {\mathbb{R}}^{\ast }$ a ${\lim }_{x\to a}g(x)=B\in {\mathbb{R}}^{\ast }$.

1. Jestliže $A<B$, pak existuje $P(a)$ takové, že pro $x\in P(a)$ je $f(x)<g(x)$.
2. Jestliže existuje $P(a)$ tak, že pro $x\in P(a)$ je $f(x)\le g(x)$, pak $A\le B$.

9) O důsledcích věty o limitním přechodu v nerovnost

Nechť $f,g:\mathbb{R}\to \mathbb{R}$, $a\in {\mathbb{R}}^{\ast }$.

1. Je-li ${\lim }_{x\to a}f(x)=0$ a existuje okolí $P(a)$ tak, že $g$ je omezená na $P(a)$. Pak ${\lim }_{x\to a}f(x)\cdot g(x)=0$.
2. Je-li ${\lim }_{x\to a}f(x)=A>0$, pak existuje okolí $P(a)$ takové, že pro $x\in P(a)$ je $f(x)>0$.

10) O sevření nebo o křídlech

Nechť $a\in {\mathbb{R}}^{\ast }$, $f,g,h:\mathbb{R}\to \mathbb{R}$. Nechť dále:

1. existuje $P(a)$ takové, že pro $x\in P(a)$ platí $h(x)\le f(x)\le g(x)$,
2. ${\lim }_{x\to a}g(x)={\lim }_{x\to a}h(x)=A\in {\mathbb{R}}^{\ast }$.

Pak také ${\lim }_{x\to a}f(x)=A$.

Navigace

Předchozí: Posloupnosti a jejich limity, limes superior, limes inferior Následující: Spojitost funkce - spojitost v bodě, spojitost na intervalu Celý okruh: 1. Teoretické základy informačních technologií