Derivace funkce a její geometrický význam - Pravidla pro derivování funkcí, derivace složené funkce, derivace inverzní funkce, derivace elementárních funkcí

Geometrický význam derivace funkce

Isibalo - Co nám říká derivace v bodě

Isibalo - Definice derivace

• Derivace v bodě vyjadřuje okamžitou rychlost růstu funkce v daném bodě

• Vezmeme-li obecně přírůstek hodnoty $\Delta x$ ($x_1-x_0$) a příslušný přírůstek $\Delta y$ ($y_1-y_0$), pak podíl $\frac{\Delta y}{\Delta x}$ je rovno průměrné rychlosti růstu v úseku $x_0$ a $x_1$

  • hodnota tohoto podílu je rovna směrnici sečny, která protíná body $[x_0,y_0]$ a $[x_1,y_1]$

• Derivace v daném bodě $a$ je limitní hodnota tohoto podílu, když se $\Delta x$ blíží nule.

  • jinými slovy, derivace je ${\lim }_{\Delta x\to 0}\frac{\Delta y}{\Delta x}$
  • tato hodnota zároveň vyjadřuje směrnici tečny v konkrétním bodě

• Dodejme, že:

  • $x_1$ = $x_0+\Delta x$
  • $y_1$ = $y_0+\Delta y$

• Na obrázku níže jsou znázorněny body $T$ a $S$ na grafu příslušné funkce a sečna, která tyto dva body protíná.

• 

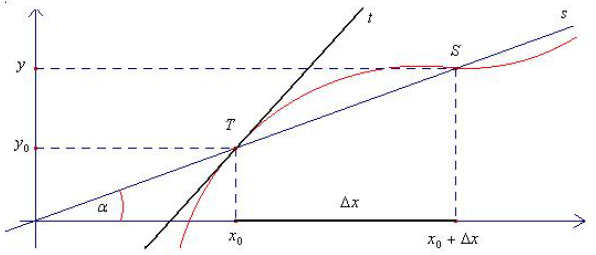
• Pokud bychom bod $S$ stále přibližovali k bodu $T$ (snižovali $\Delta x$) až by splynuly v jeden bod, vznikla by tečna, jejíž směrnice by udávala okamžitou rychlost růstu v daném bodě

• Směrnici této tečny můžeme znázornit pomocí limity: $k_t={\lim }_{\Delta x\to 0}{k}_s={\lim }_{\Delta x\to 0}\frac{\Delta y}{\Delta x}={\lim }_{\Delta x\to 0}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}$

• ve výpočtu se často využívá substituce $x=x_0+h$, tedy $h=x-x_0$ ($\Delta x$ je označen $h$,) $k_t={\lim }_{\Delta x\to 0}\frac{f(x_0+h)-f(x_0)}{h}$

• Tato limita díky svojí důležitosti dostala název derivace funkce v bodě

• Jelikož jde o směrnici tečny v daném bodě, můžeme říci, že pokud je kladná, je tečna v daném bodě rostoucí (v opačném případě klesající)

• 

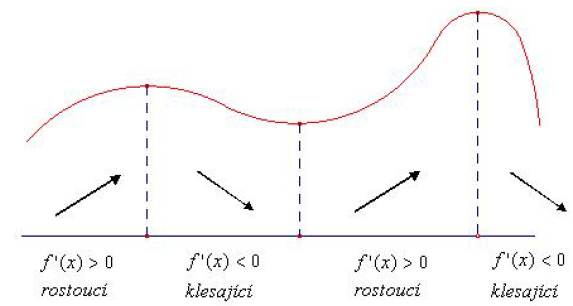
• Má-li funkce $f$ v každém bodě intervalu $(a,b)$ kladnou, resp. zápornou derivaci, je v tomto intervalu rostoucí, resp. klesající.

Derivace funkce v bodě

• Vedle pojmu limita, spojitost patří derivace mezi základní stavební prvky diferenciálního počtu
• Použití:
  • určení okamžité rychlosti dané veličiny v daném v bodě (směrnice tečny v bodě)
  • vyšetření průběhu funkce – monotonie, extrémy, konvexnost/konkávnost, inflexní body
  • optimalizace – hledání lokálního maxima/minima
  • určení některých limit pomocí l’H pravidla
• Říkáme, že funkce má v bodě $x_0\in D(f)$ derivaci, je-li definovaná v okolí bodu $x_0$ a existuje-li

$$\underset{h\to 0}{\lim }\frac{f(x_0+h)-f(x_0)}{h}$$

• Tuto limitu nazýváme derivací funkce $f$ v bodě $x_0$ a značíme ji $f^{\prime }(x_0)$ nebo $\frac{df}{dx}$ (označení zavedené G.W. Leibnizem)
• Píšeme:

$$f^{\prime }(x_0)=\underset{h\to 0}{\lim }\frac{f(x_0+h)-f(x_0)}{h}$$

• Analogicky jako limity zprava (resp. zleva) se definují derivace zprava (resp. zleva) v bodě $a$
  • značíme je $f_{+}^{\prime }(a)$, resp. $f_{-}^{\prime }(a)$.
• Pokud je hodnota limity vlastní, jedná se o vlastní derivaci, jinak mluvíme o nevlastní derivaci.
• Hodnota derivace a její existence je lokální vlastnost funkce
  • pokud existuje limita, je určena jednoznačně, každá funkce má v libovolném bodě nejvýše jednu derivaci.
• Jelikož jde o limitu, má derivace všechny vlastnosti plynoucí z limity
  • musí přitom existovat nějaká souvislost mezi existencí derivace a spojitostí funkce v bodě
  • $\to$ Má-li funkce f v bodě $x_0$ derivaci, je v tomto bodě spojitá, neplatí to však nutně opačně

Derivace funkce na množině

• Vezmeme funkci $f$ a všechny body $x$ z jejího definičního oboru, pro které definovaná derivace.
• Množina těchto bodů $M_1$ bude reprezentovat definiční obor nové funkce $g(x)$ definovaná vztahem $g(x)=f^{{}^{\prime }}(x)$ pro $x\in M_1$
• Tuto funkci nazveme derivace funkce $f$ na množině $M_1$
• Zatímco derivace v bodě je číslo, derivace funkce na množině je opět funkce

Derivace vyšších řádu

• Mějme funkci $f:y=f(x),x\in D(f)$ a množinu $D^{\prime }=\{x\in D(f)\mid \text{existuje vlastnıˊ }{f}^{\prime }(x)\}$.
• Pak $f^{\prime }:y=f^{\prime }(x),x\in D^{\prime }$ je také funkce a můžeme uvažovat o její derivaci v bodě $a\in D^{\prime }\subseteq D(f)$
• Derivaci $(f^{\prime }{)}^{\prime }(a)={\lim }_{h\to 0}\frac{f^{\prime }(a+h)-f^{\prime }(a)}{h}$ budeme nazývat druhou derivací funkce v bodě $a$ a budeme ji značit $f^{\prime \prime }(a)$.
• Obecněji:
  • Necht’ $f:\mathbb{R}\to \mathbb{R}$ má vlastní derivaci $f^{(n-1)},n\in \mathbb{N}$ v nějakém $U(a),a\in D(f)$, pak definujeme n-tou derivaci funkce v bodě $a$ jako $f^{(n)}(a)=(f^{(n-1)}{)}^{\prime }(a),$
  • pokud má pravá strana smysl. Dále klademe $f^{(0)}=f$.

Základní vlastnosti derivace

1. Necht’ $f:\mathbb{R}\to \mathbb{R},a\in \mathbb{R}$. Funkce $f$ má v bodě $a$ derivaci $f^{\prime }(a)$ právě když má v bodě $a$ obě jednostranné derivace a platí $f_{+}^{\prime }(a)=f_{-}^{\prime }(a)=A$. Je pak $f^{\prime }(a)=A$.

2. Má-li $f:\mathbb{R}\to \mathbb{R}$ v bodě $a\in \mathbb{R}$ vlastní derivaci zprava $f_{+}^{\prime }(a)$, je v tomto bodě spojitá zprava.

3. Necht’ $f$ má v bodě $a$ obě vlastní jednostranné derivace (není nutné, aby si byly rovny). Pak je v $a$ spojitá.

   • neplatí naopak (derivace $\to$ spojitá, ale neplatí spojitá $\to$ derivace)
   • např. funkce $f:x=|x|$, $D(x)=\mathbb{R}$ nemá derivaci v bodě $x=0$
     • tato funkce sice má obě jednostranné limity, které jsou rovny $f(0)$, ale má odlišné jednostranné derivace $f_{-}^{{}^{\prime }}(0)=-1$, zatímco $f_{+}^{{}^{\prime }}(0)=1$
     • je spojitá, ale nemá derivaci

4. O derivaci součtu, součinu a podílu

• Necht’ $f,g:\mathbb{R}\to \mathbb{R}$ mají v $a\in \mathbb{R}$ vlastní derivace $f^{\prime }(a)$ a $g^{\prime }(a)$. Pak
  1. $(f+g{)}^{\prime }(a)=f^{\prime }(a)+g^{\prime }(a),$
  2. $(f\cdot g{)}^{\prime }(a)=f^{\prime }(a)\cdot g(a)+f(a)\cdot g^{\prime }(a),$
  • Je-li navíc $g(a)\ne 0$, platí $${\left(\frac{f}{g}\right)}^{\prime }(a)=\frac{f^{\prime }(a)\cdot g(a)-f(a)\cdot g^{\prime }(a)}{g^2(a)}.$$

5. O derivaci složené funkce

• Necht’ $f:\mathbb{R}\to \mathbb{R}$ má vlastní derivaci v bodě $a\in \mathbb{R}$ a $g:\mathbb{R}\to \mathbb{R}$ vlastní derivaci v bodě $f(a)$. Pak existuje vlastní derivace složené funkce $g\circ f$ v bodě $a$: $(g\circ f{)}^{\prime }(a)=g^{\prime }(f(a))\cdot f^{\prime }(a).$
• Nejprve vezmeme vnější funkci, tu derivujeme jako funkci jednoduchého argumentu, a pak pokračujeme násobením derivací vnitřní funkce.
• Někdy se tomuto pravidlu derivování složené funkce říká také řetězové pravidlo.
• Obecně: vždy postupujeme od vnější funkce, tu derivujeme tak, jako by byla jednoduchého argumentu
  • pak postupujeme dovnitř a derivujeme další funkce, až se dostaneme k poslední, vnitřní funkci, která již není složená
  • jednotlivé derivace vynásobíme

6. O derivaci inverzní funkce

• Necht’ $f:\mathbb{R}\to \mathbb{R}$ je spojitá a ryze monotónní na intervalu $I$, necht’ $f^{-1}$ je její inverzní funkce na $I$ a necht’ $a$ je vnitřní bod $I$. Jestliže $f^{\prime }(a)\in \mathbb{R}\setminus \{0\}$, pak $(f^{-1}{)}^{\prime }(a)=\frac{1}{f^{\prime }(a)}.$

Derivace elementárních funkcí

• Pro výpočet derivace elementárních funkcí existují vzorce odvozené na základě definice derivace jako limity

• 

Navigace

Předchozí: Vlastnosti spojitých funkcí, spojitost složené a inverzní funkce Následující: Průběh funkce - základní věty diferenciálního počtu, extrémy funkce, konvexní a konkávní křivky, asymptoty Celý okruh: 1. Teoretické základy informačních technologií