Pojem množina
-
Množina je objekt, který se skládá z jiných objektů, tzv. prvků množiny
-
Množina je jednoznačně daná prvky, které obsahuje - nemá tedy smysl hovořit o pořadí prvků v množině, nebo kolikrát je daný prvek v množině
-
Množina je matematickým protějškem k pojmům soubor, seskupení, …
-
Množiny označujeme velkými písmeny a jejich prvky malými
- znamená, že je prvkem množiny
-
Zápis množin lze těmito základními způsoby:
- Výčtem prvků , množina obsahuje právě prvky
- Charakteristická vlastnost , množina obsahuje prvky splňující vlastnost
-
Systém množin = množina, jejíž prvky jsou znovu množiny
Vztahy mezi množinami
- Rovnost
- Označujeme symbolem ""
- Pro každé platí: , právě když
- Dvě množiny obsahují stejné prvky
- Když říkáme, že množina se rovná množině
- platí, právě když platí zároveň a
- Inkluze
- Označujeme symbolem ""
- Pro káždé platí: jestliže , pak
- Všechny prvky množiny jsou také prvky množiny
- Když říkáme, že množina je podmnožinou množiny
- Někdy je výhodné psát , abychom označili, že a
Operace s množinami
- Mezi základní operace s množinami patří průnik, stejnocení a rozdíl
- Průnik
- Označujeme symbolem ""
- a
- Prvek patří do , právě když patří do a zároveň do
- Společné prvky
- Množiny A a B se nazývají navzájem disjunktní právě když
- Sjednocení
- Označujeme symbolem ""
- nebo
- Prvek patří do , právě když patří do nebo do
- Spojení všech prvků v množinách
- Rozdíl
- Označujeme symbolem ""
- a
- Prvek patří do , právě když patří do , ale nepatří do
Vennovy diagramy
- Lze na nich ilustrovat základní operace a vztahy mezi množinami
- Umožňují názornou představu
Potenční množina
- Značí se
- Množina, jejímiž prvky jsou právě všechny podmnožiny dané množiny
- Je-li konečná, pak
- Vždy obsahuje prázdnou množinu (), protože ta je podmnožinou každé množiny
Příklad
Kartézský součin
- Kartézský součin množin je množina všech uspořádaných -tic prvků z těchto množin
- Je-li , pak píšeme a říkáme -tá kartézská mocnina množiny
- Velikost je
Speciální množiny
- Speciální množinou je tzv. prázdná množina, označující se . Tato množina neobsahuje žádný prvek, tedy pro každý prvek platí:
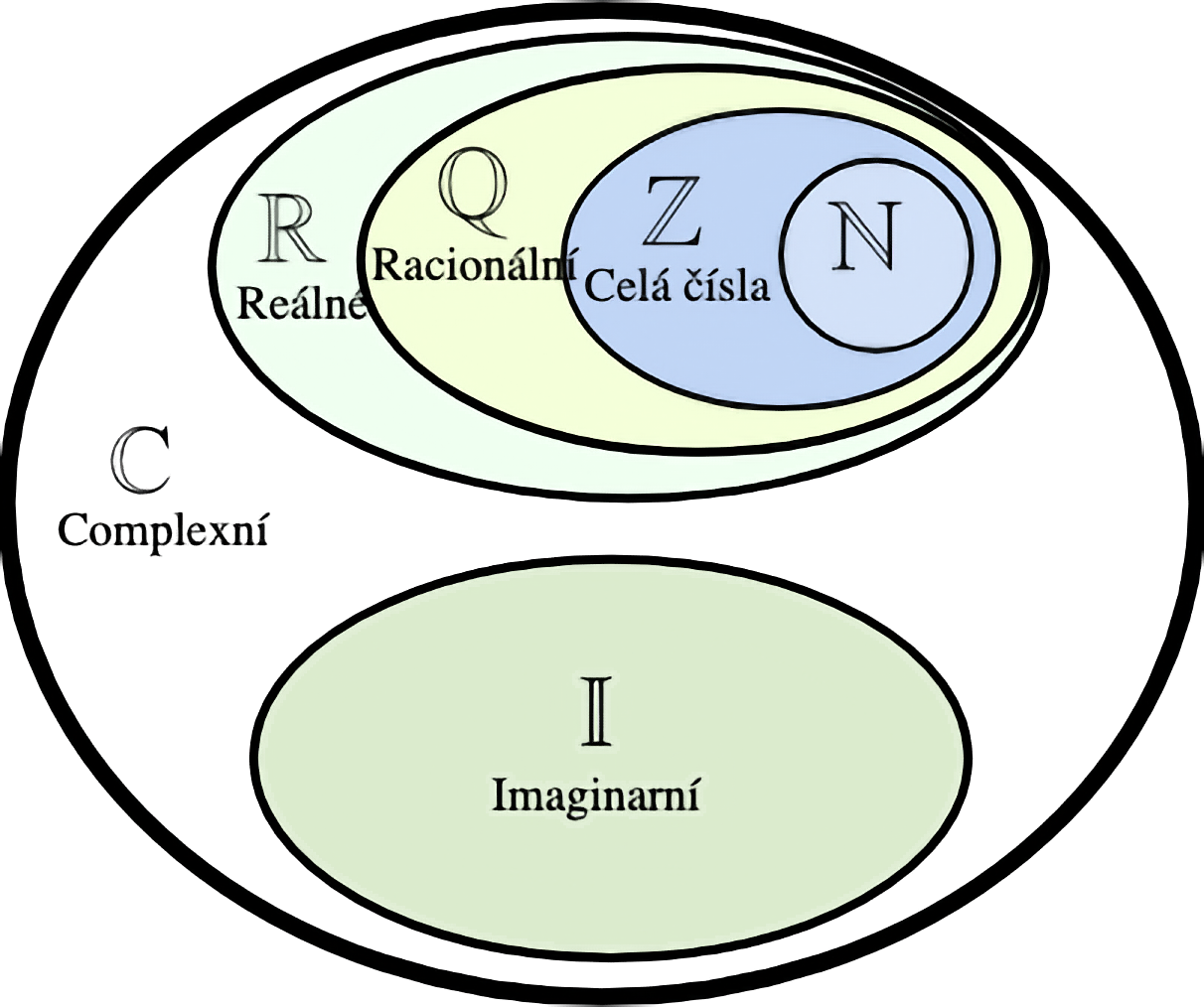
Význačné číselné množiny
- Přirozená čísla -
- Jsou používána pro počítání a pořadí.
- Celá čísla -
- Zahrnují přirozená čísla, jejich záporné protějšky a nulu.
- Racionální čísla -
- Čísla, která lze vyjádřit jako podíl dvou celých čísel (, kde a ).
- Mohou být zlomky nebo celá čísla.
- Iracionální čísla
- Zahrnuje čísla, která nelze vyjádřit jako podíl dvou celých čísel.
- Reálné čísla -
- Všechna racionální a iracionální čísla.
- Reálná čísla reprezentují všechny možné hodnoty na číselné ose.
Množiny konečné/nekonečné a spočetné/nespočetné
-
Množiny se dělí na:
- Konečné
- Existuje přirozené číslo tak, že prvky v množině lze jednoznačně očíslovat
- Číslo určuje počet prvků v množině (velikost množiny)
- Značení
- Nekonečné
- Není-li konečná
- Značení
- Konečné
-
Množina může být:
- Spočetná
- Pokud je konečná nebo existuje bijekce
- Jinými slovy, množina je spočetná, pokud její prvky lze jednoznačně přiřadit k prvkům množiny přirozených čísel. Tedy pokud existuje bijekce mezi touto množinou a podmnožinou
- Značení
- Pokud je konečná nebo existuje bijekce
- Nespočetná
- Není-li spočetná
- Nespočetné množiny jsou vždy nekonečné
- Důkaz nespočetnosti lze například pomocí Cantorovy diagonální metody
- Spočetná
Příklad spočetné a nespočetné množiny
- Množina celých čísel je nekonečná, ale je spočetná, protože můžeme zkonstruovat bijekci s množinou .
- Množina reálných čísel je nespočetná. To lze dokázat pomocí Cantorova diagonálního argumentu, který ukazuje, že žádná bijekce mezi a neexistuje.
Navíc - Cantorova diagonální metoda
Navigace
Předchozí: Úplné konjunktivní a disjunktivní normální formy Následující: Relace, binární relace a jejich reprezentace, operace s relacemi Celý okruh: 1. Teoretické základy informačních technologií