Posloupnost
- Každé zobrazení nazýváme číselná posloupnost
- kde je libovolná množina libovolných objektů
- pokud je obor hodnot číselný, pak mluvíme o číselné posloupnosti
- Posloupnost je konečná, jestliže je definičním oborem množina , kde
- takové posloupnosti označujeme jako uspořádáné -tice
- Funkční hodnotu funkce v bodě nazýváme -tý člen posloupnosti a značíme apod.
- Posloupnost s -tým členem pak zapisujeme nebo jen
- Neformálně lze chápat jako kolekci hodnot, ve které jsou prvky dány svým pořadím (sekvence)
Způsoby zadání posloupnosti
- Číselná posloupnost bývá zadána:
- Několika prvními členy
- z kterých jsou zřejmé následující členy
- Předpisem vyjadřující n-tý člen
- Rekurentně
- Členy posloupnosti jsou určeny pomocí jednoho nebo více předcházejících členů
- Typickým příkladem je Fibonacciho posloupnost:
- Několika prvními členy
Podposloupnost
- Posloupnost se nazývá podposloupnost , právě když existuje posloupnost přirozených čísel tak, že je .
Speciální posloupnosti
Aritmetická posloupnost
- Posloupnost se nazývá aritmetická, právě když existuje číslo takové, že pro každé platí
- Číslo nazýváme diference aritmetické posloupnosti.
Geometrická posloupnost
- Posloupnost se nazývá geometrická, právě když existuje takové , že pro libovolné platí
- Číslo nazýváme kvocientem geometrické posloupnosti.
Monotónnost posloupnosti
- Posloupnost se nazývá
- Má-li posloupnost některou z prvních 4 vlastností, nazýváme ji monotónní.
- Je-li posloupnost rostoucí nebo klesající, nazýváme ji ryze monotónní
Omezenost posloupnosti
- Posloupnost se nazývá
Limity posloupnosti
- Zkoumáme chování posloupnosti pro velká přirozená čísla
- Jedná se o hodnotu, ke které se posloupnost přibližuje, postupuje-li do nekonečna
Konečné limity posloupnosti
Definice
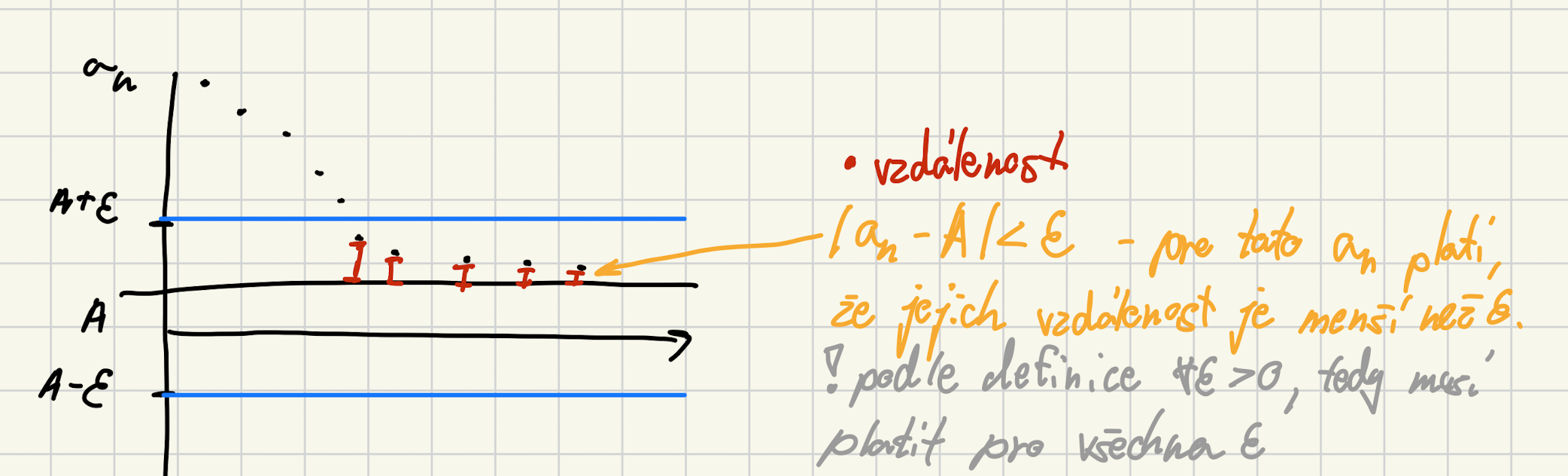
Číslo se nazývá limita posloupnosti právě když
- Píšeme
- Takovou posloupnosti pak nazýváme konvergentní
- říkáme že posloupnost konverguje k
- např. geometrická posloupnost , pro jejíž kvocient platí , je konvergentní a , konverguje tedy k
- Místo píšeme také , čteme posloupnost konverguje ke své limitě
Nekonečné limity posloupnosti
- Posloupnost , která nemá konečnou limitu, nazýváme divergentní
Definice
Říkáme, že posloupnost má limitu , právě když Píšeme . Analogicky definiujeme .
Vlastnosti limit
Vlastnosti limit
- Každá posloupnost má nejvýše jednu limitu.
- posloupnost buď limitu nemá (je divergentní) nebo má právě jednu
- Každá konvergentní posloupnost je omezená
- Nechť a jsou konvergentní posloupnosti a nechť a . i) ii) iii) (pro ; ) iv) pro
Isibalo - Věty o limitách posloupností
Limes inferior a Limes superior
- Tyto pojmy můžeme chápat jako omezení zespoda a seshora pro hodně velké (v nekonečnu)
- Posloupnost těchto mezí buďto nabývá nebo se nekonečně blíží v konečném počtu případů
- Na rozdíl od limity, limes inferior i limes superior vždy existují
- Limita posloupnost existuje, jestliže
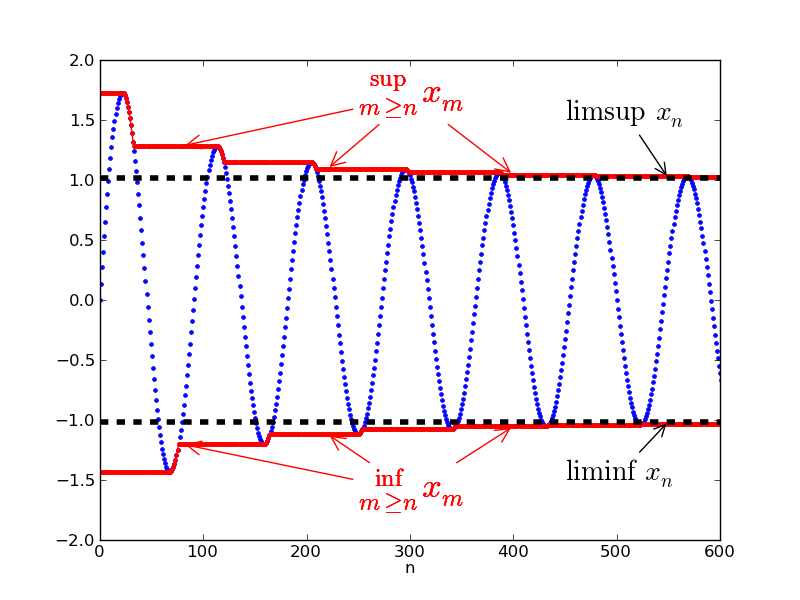
Limes superior
- Nechť je posloupnost reálných čísel. Pak definujeme
- Tuto hodnotu nazýváme limes superior posloupnosti .
- Alternativní zápis:
Limes inferior
- Nechť je posloupnost reálných čísel. Pak definujeme
- Tuto hodnotu nazýváme limes inferior posloupnosti .
- Alternativní zápis:
Navigace
Předchozí: Funkce jedné reálné proměnné, základní vlastnosti Následující: Limita funkce včetně nevlastních, jednostranné limity Celý okruh: 1. Teoretické základy informačních technologií