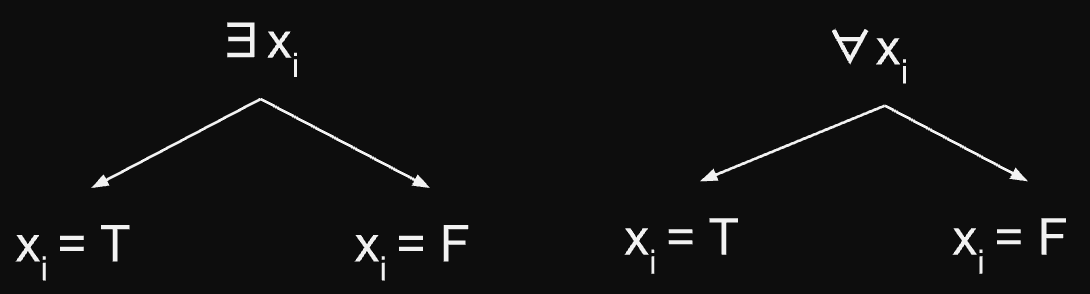Třída PSPACE, její vztah k třídám P a NP, PSPACE-úplné problémy

• Třídou prostorové složitosti $S(f)$, rozumíme třídu těch problémů, které jsou řešeny TS s prostorovou složitostí v $O(f)$
• PSPACE:
  • Třída obsahující všechny problémy řešitelné algoritmy s polynomiální prostorovou složitostí.
• NPSPACE:
  • Třída obsahující všechny problémy řešitelné nedeterministickými algoritmy s polynomiální prostorovou složitostí.

Vzájemný vztah

$PTIME\subseteq NPTIME\subseteq PSPACE=NPSPACE$

1. PTIME $\subseteq$ NPTIME
   • Přeš velké úsilí věděcké komunity, zatím nebylo dokázáno, že PTIME $=$ NPTIME, ani že PTIME $\ne$ NPTIME.
   • To znamená, že stále existuje možnost, že některé problémy, které jsou řešitelné nedeterministickými algoritmy v polynomiálním čase, mohou být řešitelné i deterministickými algoritmy v polynomiálním čase, nebo naopak.
   • Nicméně existuje mnoho problémů, u kterých se věří, že jsou řešitelné nedeterministickými algoritmy v polynomiálním čase, ale nebylo nalezeno žádné deterministické řešení v polynomiálním čase. Tyto problémy jsou považovány za “typické” pro třídu NPTIME.
   • Mezi takové problémy patří například problém nalezení Hamiltonovské kružnice v grafu.
2. NPTIME $\subseteq$ PSPACE
   • Pro libovolnou funkci $f$ je $T(f(n))\subseteq S(f(n))$
   • Např. TS očividně navštíví při výpočtu nejvýše tolik políček, kolik udělá kroků
3. PSPACE $=$ NPSPACE
   • Platí podle Savitchovi věty

Důkaz Savitchovi věty

$t=c{n}^k$

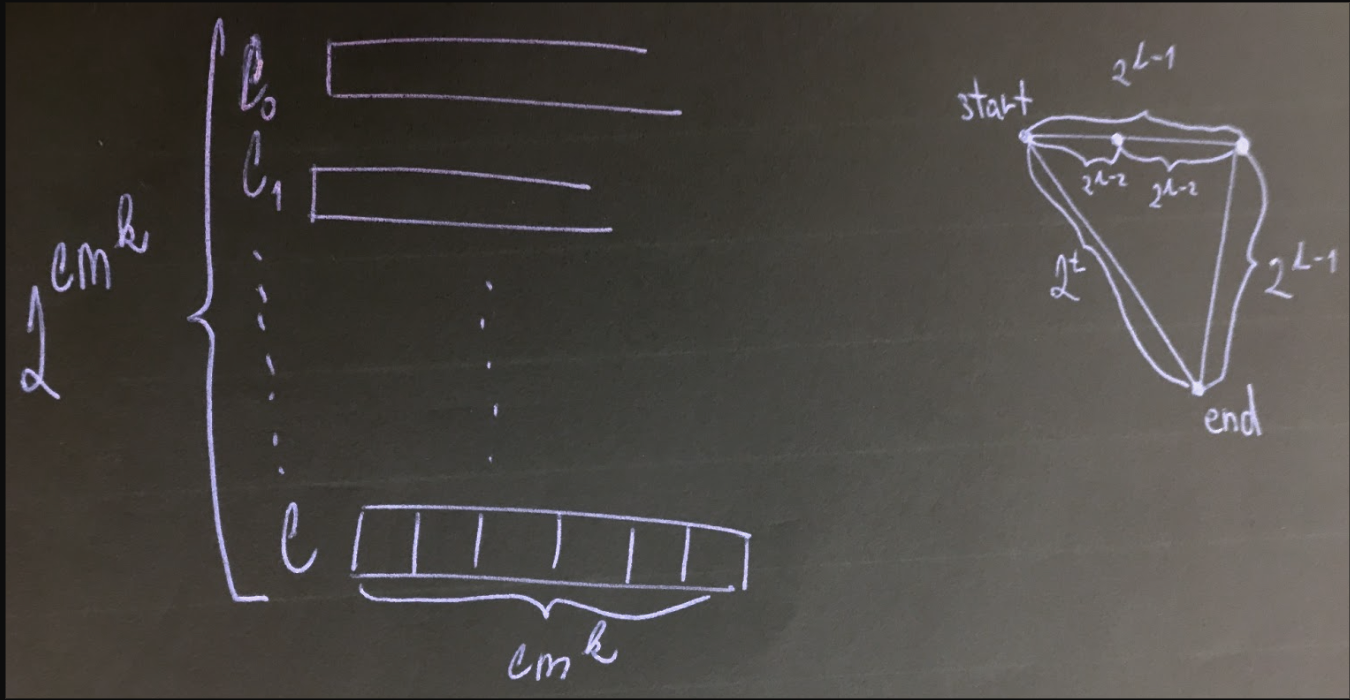
• Z počáteční konfigurace do poslední se dostaneme ve $2^t$ krocích.
• Z počáteční konfigurace do prostřední se dostaneme ve $2^{t-1}$ krocích a z prostřední do koncové $2^{t-1}$ krocích
• Proces dělení budeme opakovat, dokud se nedostaneme z jedné konfigurace do druhé v jednom kroku (z počáteční do $\frac{1}{4}$ se dostaneme v $2^{t-2}$ krocích, atd.)
• Počet konfigurací vzhledem k výšce stromu ${\log }_2{n}^k=n^k{\log }_{2}2=n^k$
• Což znamená: $c{n}^k\ast c{n}^k=c^2{n}^{2k}$ tudíž $O(n^{2k})$
  • $c{n}^k$ - počet buněk v jedné konfiguraci
  • $c{n}^k$ - počet konfigurací vzhledem k výšce stromu

Polynomiální redukce

• Mějme $ANO/NE$ problémy $P_1,P_2$. Řekneme, že problém $P_1$ je polynomiálně převeditelný na problém $P_2$, $P_1{\le }_p{P}_2$, jestliže existuje (převádějící) polynomiální algoritmus $A$, který pro libovolný vstup $w$ problému $P_1$ sestrojí vstup problému $P_2$, $A(w)$, přičemž platí, že odpověď na otázku problému $P_1$ pro vstup $w$ je $ANO$ právě tehdy, když odpověď na otázku problému $P_2$ pro vstup $A(w)$ je $ANO$.
• Problém $Q$ nazveme PSPACE-tězký, pokud každý problém ve třídě PSPACE lze na problém $Q$ polynomiálně převést, tedy pokud platí $\forall P\in \text{ PSPACE }:P{\le }_{p}Q$.
• Problém $Q$ nazveme PSPACE-úplným, pokud je PSPACE-tězký a náleží do třídy PSPACE

Příklady PSPACE - úplných problémů

Q-SAT (QBF)

Název: Q-SAT Vstup: Formule $(\exists x_1)(\exists x_2)(\exists x_3)(\forall x_4)...(\exists x_{2n-1})(\forall x_{2n})F(x_1,x_2,...,x_{2n})$, kde $F(x_1,x_2,...,x_{2n})$ je booleovská formule v konjunktivní normální formě. Otázka: Je daná formule pravdivá?

Eq-NFA (ekvivalence nedeterministických konečných automatů)

Název: Eq_NFA Vstup: Nedeterministické konečné automatu $A_1$ a $A_2$ Otázka: Je $L(A_1)=L(A_2)$?

Eq-RegExp (ekvivalence regulárních výrazů)

Název: Eq-RegExp Vstup: Regulární výrazy $E_1$ a $E_2$ Otázka: Je $E_1=E_2$?

Prokázání, že problém QBF je v PSPACE

• Při vypracovávání ohodnocení formule $F$, vytvářím strom rekurze
• Pokud je v rekurzi $\exists$ stačí když platí jedna větev
• Pokud je v rekurzi $\forall$ musí platit obě větve!
• QBF $\in$ PSPACE, protože jediné, co nám stačí je pamatovat si aktuální větev výpočtu

Navigace

Předchozí: Příklady NP-úplných problémů, dokazování NP-úplnosti Následující: Algoritmus, problém, časová složitost algoritmu v nejhorším a průměrném případě Celý okruh: 1. Teoretické základy informatiky