Určitý integrál
- Existuje několik definic určitého integrálu:
- Cauchyův
- Newtonův,
- Riemannův (nejčastější) - zobecnění Cachyuova integrálu,
- Lebesgueův…
- Definice se liší množinou funkcí, pro které platí
- Na rozdíl od neurčitého integrálu, kde výsledkem je množina primitivních funkcí, je výsledkem určitého integrálu číslo, které můžeme interpretovat jako obsah plochy pod křivkou grafu funkce na intervalu
- určitý integrál uvažujeme na uzavřeném intervalu, na níž je funkce omezena
- říkáme určitý integrál od do
- Využití pro výpočet:
- obsahu plochy pod křivkou grafu (rovinného útvaru),
- délky křivek,
- objemy rotačních těles, pláště těles,…
- jiné aplikace ve fyzice, chemii
Poznámka
Idea výpočtu obsahu plochy pro vymezený úsek grafu:
- Úsek grafu rozdělíme na podintervalů stejné délky
- (obecně stejné délky mít nemusí)
- Pro každý interval můžeme uvažovat obdélník, jehož základna je dána dělením a výška je dána některou funkční hodnotou na daném podintervalu
- např. lokální maximum/minimum
- Odhad (aproximace) obsahu celé plochy spočítáme jako součet obsahů ploch jednotlivých obdélníků
- Je přitom zřejmé že, pokud vezmeme jako výšky jednotlivých obdélníků lokální maxima/minima, je tento odhad nepřesný
- Přesnější odhad získáme jemnějším rozdělením na více podintervalů (užších obdélníků)
Obsah rovinného útvaru
-
Uvažme funkci , která je spojitá a kladná na intervalu . Potom určitý integrál funkce udává obsah rovinného útvaru ohraničeného grafem funkce , osou a přímkami a
-
Jestliže funkce nabývá na intervalu záporných hodnot, pak je obsah vypočítán jako
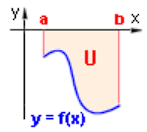
-
Jestliže funkce nabývá na intervalu kladných i záporných hodnot, pak stačí tento interval rozdělit na dílčí intervaly, ve kterých nabývá funkce pouze kladných (resp. záporných) hodnot - spočítáme obsahy jednotlivých dílčích intervalů dle výše uvedených úvah a sečteme
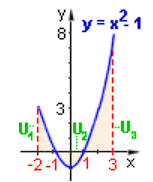
- Je-li rovinný útvar omezený spojitými funkcemi shora a funkcí zdola (platí pro ), pak pro obsah platí: - tento vztah platí i případě, že funkce v některých částech nabývají záporných hodnot
- pokud se navíc funkce a neprotínají stačí si výpočet zjednodušit na
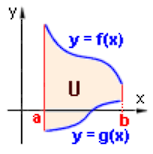
- Příklad výpočtu:
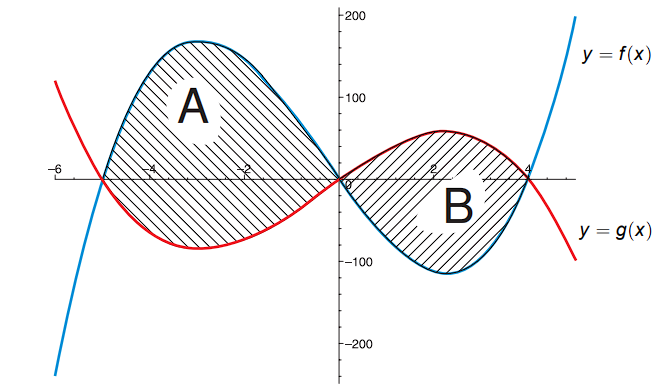
- Obsah plochy A + B omezené funkcemi a z výše uvedeného obrázku bychom spočítali následovně: 1. Vyhledáme průsečíky funkcí na daném intervalu: a 2. Ze znalosti vzájemné velikost a spočítáme 3. Pokud bychom uspořádání a na určeném intervalu neznali, stačí:
Délka rovinné křivky
- Nechť funkce je na intervalu spojitá a má definovanou derivaci, pak pro délku jejího grafu platí:
Objem rotačního tělesa
- Vezmeme-li rovinný útvar a necháme ho rotovat kolem osy , vznikne nám rotační těleso, jehož objem můžeme spočítat pomocí určitého integrálu
- Nechť rotační těleso vznikne rotací křivky funkce kolem osy na intervalu , pak pro jeho objem platí:
- Pokud bychom chtěli spočítat objem rotačního tělesa ohraničený dvěma funkcemi a , pak pro jeho objem platí:
Obsah rotační plochy
- Pomocí určitého integrálu spočítáme i obsah pláště rotačního tělesa:
Navigace
Předchozí: Riemannův určitý integrál - definice, základní věta integrálního počtu, metody výpočtu Následující: Algoritmus, problém, časová složitost algoritmu v nejhorším a průměrném případě Celý okruh: 1. Teoretické základy informačních technologií