Geometrický význam derivace funkce
-
Derivace v bodě vyjadřuje okamžitou rychlost růstu funkce v daném bodě
-
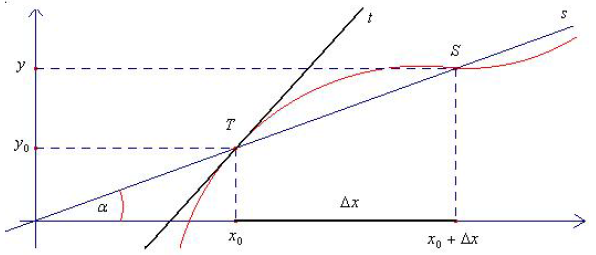
Vezmeme-li obecně přírůstek hodnoty () a příslušný přírůstek (), pak podíl je rovno průměrné rychlosti růstu v úseku a
- hodnota tohoto podílu je rovna směrnici sečny, která protíná body a
-
Derivace v daném bodě je limitní hodnota tohoto podílu, když se blíží nule.
- jinými slovy, derivace je
- tato hodnota zároveň vyjadřuje směrnici tečny v konkrétním bodě
-
Dodejme, že:
- =
- =
-
Na obrázku níže jsou znázorněny body a na grafu příslušné funkce a sečna, která tyto dva body protíná.
-
-
Pokud bychom bod stále přibližovali k bodu (snižovali ) až by splynuly v jeden bod, vznikla by tečna, jejíž směrnice by udávala okamžitou rychlost růstu v daném bodě
-
Směrnici této tečny můžeme znázornit pomocí limity:
-
ve výpočtu se často využívá substituce , tedy ( je označen ,)
-
Tato limita díky svojí důležitosti dostala název derivace funkce v bodě
-
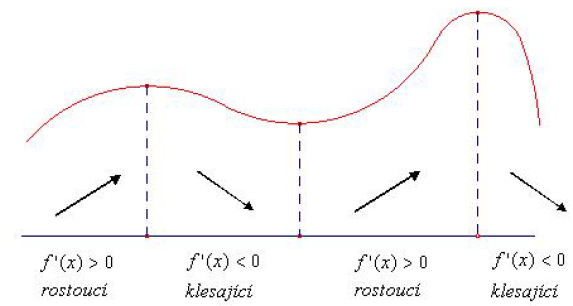
Jelikož jde o směrnici tečny v daném bodě, můžeme říci, že pokud je kladná, je tečna v daném bodě rostoucí (v opačném případě klesající)
-
-
Má-li funkce v každém bodě intervalu kladnou, resp. zápornou derivaci, je v tomto intervalu rostoucí, resp. klesající.
Základní věty diferenciálního počtu
Isibalo - Motivace přůběhu funkce
- Nyní si uvedeme několik vět, které nám pomohou jednoduše zjišťovat, na kterých intervalech je funkce rostoucí (klesající), resp. jak dohledat lokální extrémy těchto funkcí.
Stacionární bod
- Bod nazýváme stacionárním bodem funkce , existuje-li a je-li .
- Tyto body někdy označovány výstižněji jako body podezřelé z extrémů
- nulová první derivace je nutnou podmínkou pro existenci extrému
Monotónnost funkce
- Říkáme, že funkce je rostoucí v bodě právě tehdy, když existuje takové, že
- Obdobně můžeme definovat pojmy klesající, neklesající a nerostoucí.
- , resp. značí levé, resp. pravé prstencové okolí bodu .
Postačující podmínka pro lokální monotonii
- Necht’ a existuje . Pak
- je-li , je v rostoucí,
- je-li , je v klesající.
O monotonii na intervalu
- Nechť je na intervalu spojitá a nechť v každém vnitřním bodě intervalu existuje derivace, pak platí:
- Funkce je na intervalu rostoucí (klesající), právě když pro všechny vnitřní body je ().
- Funkce je na intervalu neklesající (nerostoucí), právě když pro všechny vnitřní body je ().
- Je-li pro každý vnitřní bod intervalu , je konstantní na .
Lokální extrémy funkce
- Říkáme, že funkce má v bodě
- ostré lokální maximum právě tehdy, když existuje takové, že ,
- ostré lokální minimum právě tehdy, když existuje takové, že .
- Pokud zaměníme ostré nerovnosti za neostré, dostaneme definici pro lokální maximum, resp. lokální minimum
- Obecně mluvíme o lokálních extrémech
- Jedná se o body, ve kterých funkce mění svojí monotonii
Isibalo - Co je to monoténnost a extrémy
Fermatova věta - nutná podmínka pro lokální extrém
- Necht’ a existuje . Má-li funkce v bodě extrém, pak .
- Znaménková změna první derivace ovlivňuje monotonii funkce
- Tyto body označujeme jako stacionární body
- Výstižněji také “body podezřelé z extrému”.
Poznámka
- Tvrzení nám sice zajišťuje podmínku, za které by mohl nastat v bodě extrém, nic nám však neříká, zda tam opravdu nastane.
- kladná (záporná) derivace v bodě funkce v bodě roste (klesá),
- extrém v bodě nulová derivace v bodě.
- Obráceně to neplatí, což si ukážeme na příkladu.
- Uvažujme funkci , v bodě . Derivace a tedy , přitom v libovolném levém okolí nuly platí:
Poznámka
- Extrému může nabýt funkce v bodě, v němž derivace vůbec neexistuje
- Např. funkce nemá v bodě derivaci, má zde pouze jednostranné derivace (jednostranné limity) a .
- Přitom víme, že má v tomto bodě minimum ().
- Bylo by tedy žádoucí poznat nějaké kritérium, které by nám nejen zaručilo, že v daném bodě extrém nastane, ale také nám objasnilo, o jaký extrém se bude jednat
Postačující podmínky pro lokální maximum
- Nechť , je spojitá v bodě . Pak:
- Je-li rostoucí na a klesající na , pak má v bodě ostré lokální maximum.
- Je-li a , pak má v bodě ostré lokální maximum.
Postačující podmínky pro lokální minimum
- Nechť , je spojitá v bodě . Pak:
- Je-li klesající na a rostoucí na , pak má v bodě ostré lokální minimum.
- Je-li a , pak má v bodě ostré lokální minimum.
Isibalo - Proč používáme první derivace
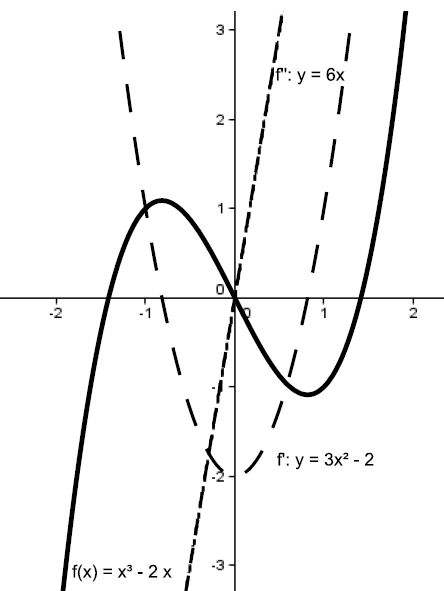
Derivace vyšších řádů
- Derivaci budeme nazývat druhou derivací funkce v bodě .
- Indukcí pak můžeme zavést derivace vyšších řádů:
- Nechť má vlastní derivaci , v nějakém okolí bodu z definičního oboru . Pak definujeme n-tou derivaci funkce v bodě jako
- Má-li smysl, klademe .
Určení monotonie a extrémů pomocí derivace vyšších řádů
- Tvrzení, které nám mnohdy může pomoci rozhodnout o monotonii či extrému v bodě v případě, kdy prvních derivací v bodě je nulových.
- Nechť , a existuje , takové, že a . Pak:
- Je-li sudé a , pak má v bodě ostré lokální minimum.
- Je-li sudé a , pak má v bodě ostré lokální maximum.
- Je-li liché a , pak je v bodě rostoucí.
- Je-li liché a , pak je v bodě klesající.
- Mnohdy stačí najít body podezřelé z extrému a spočítat druhou derivaci v těchto bodech.
- Pokud bude záporná, jedná se o ostré lokální maximum, pokud bude kladná, můžeme ho prohlásit za ostré lokální minimum.
Postačující podmínky pro lokální extrémy.
- Nechť a nechť existuje v bodě druhá derivace.
- Je-li , má funkce v bodě ostré lokální maximum
- posloupnost směrnic tečen totiž klesá
- Je-li , má funkce v bodě ostré lokální minimum
- posloupnost směrnic tečen totiž roste
- Je-li , má funkce v bodě ostré lokální maximum
Věty o střední hodnotě
- Tyto věty mají velký význam v dokazování dalších vět
- např. L’Hospitalovo pravidlo, určitý integrál…
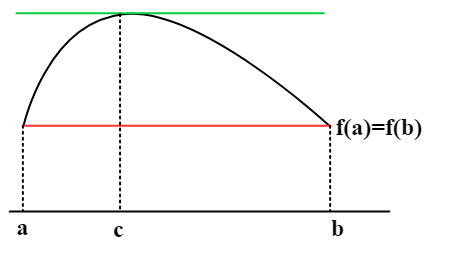
Rolleova věta
- Nechť funkce má následující vlastnosti:
- Je spojitá na uzavřeném intervalu .
- Je diferencovatelná na otevřeném intervalu .
- Platí .
- Potom v otevřeném intervalu existuje alespoň jeden bod takový, že
- v nějakém bodě změní monotonii (rovnost koncových bodů)
- Věta sama zaručuje pouze existenci alespoň jednoho takového bodu, neumožňuje nám však ani tento bod určit, ani stanovit počet takových bodů
Lagrangeova věta
- Nechť funkce má následující vlastnosti:
- Je spojitá na uzavřeném intervalu .
- Má derivaci na otevřeném intervalu .
- Potom v otevřeném intervalu existuje alespoň jeden bod takový, že
- Geometrická interpretace:
- spojíme-li přímkou body a potom mezi body a existuje alespoň jeden bod , v níž je tečna ke grafu funkce je rovnoběžná s přímkou
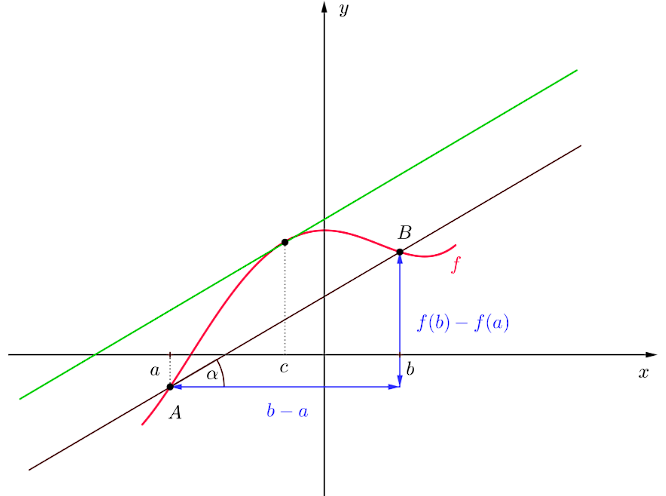
- Fyzikální interpretace
- Uvážíme-li nějakou veličinu, která se v čase mění podle hladké funkce, pak existuje okamžik uvnitř časového intervalu , kdy je okamžitá změna této veličiny rovna průměrné změně za celý časový interval - střední hodnota
Cauchyova věta
- Nechť funkce , mají následující vlastnosti:
- jsou spojité na intervalu
- mají v každém bodě intervalu vlastní derivaci
- pro všechna platí .
- Pak existuje bod takový, že platí:
- Jedná se o zobecnění Lagrangeovy věty o střední hodnotě
Prostost funkce
- Nechť funkce vyhovuje podmínkám Lagrangeovy věty a navíc ať pro všechna . Potom je funkce prostá na .
- Důkaz:
- funkce je na množině prostá, jestliže
- předpokládejme že a že , pak ale podle Lagrangeovy věty
- to je však spor s podmínkou ” pro všechna “
Konstantnost funkce
- Funkce je konstantní na intervalu , právě když má v tomto intervalu derivaci a platí pro všechna .
l’Hospitalovo pravidlo
- Nechť , . Nechť existuje
- a nechť je splněna jedna z následujících podmínek:
- ,
- .
- Pak existuje a platí
Konvexní a konkávní funkce
-
Uvažujme obecnou funkci
-
Zvolíme-li na grafu funkce tři různé body , , takové, že . Vidíme, že bod leží pod přímkou .
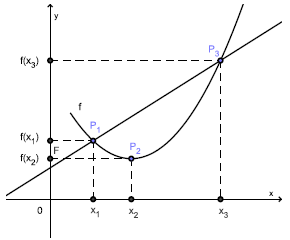
-
Má-li přímka rovnici , pak výrok „ leží pod přímkou ” znamená, že leží v polorovině ).
-
Rovnice přímky je následovná:
- Pokud bod má ležet pod touto přímkou, stačí zaměnit „=” za „<” a obecný bod o souřadnicích za náš .
- Analogickou úvahu lze provést pro bod ležící nad přímkou.
Isibalo - Co je to konvexnost a konkávnost
Isibalo - Proč druhá derivace
Definice
- Nechť je definována na intervalu . Říkáme, že funkce je na intervalu
- ryze konvexní právě tehdy, když pro libovolnou trojici , platí
- ryze konkávní právě tehdy, když pro libovolnou trojici , platí
- Ověření těchto vlastností pomocí uvedených postupů je však náročné, nalézt a ověřit je lze pomocí druhé derivace (sudé)
O konvexnosti a konkávnosti funkce na intervalu
-
Nechť je spojitá na intervalu a nechť v každém vnitřním bodě tohoto intervalu existuje druhá derivace. Pak
- Je-li v každém vnitřním bodě intervalu , je ryze konvexní na .
- posloupnost směrnic tečen roste
- Je-li v každém vnitřním bodě intervalu , je ryze konkávní na .
- posloupnost směrnic tečen klesá
- ”Do konkávy do kávu nenaliješ” :)
- Je-li v každém vnitřním bodě intervalu , je lineární na .
- Je-li v každém vnitřním bodě intervalu , je ryze konvexní na .
-
Bod, kde se konvexnost mění na konkávnost nebo naopak, nazveme inflexním bodem.
Nutná podmínka pro existenci inflexního bodu
- Je-li bod inflexním bodem funkce a má-li funkce v tomto bodě vlastní druhou derivaci, pak .
- Jedná se o bod, ve které se funkce přeměňuje z konkávní na konvexní nebo naopak
Asymptota
- Při vyšetřování průběhu funkce a především pro přesnější kreslení jejího grafu je dobré znát přímky, kterým se graf funkce v okolí některých zajímavých bodů podobá
- Zjednodušeně řečeno, asymptota je přímka, ke které se graf funkce blíží, ale nikdy se jí nedotkne.
Isibalo - Co jsou to asymptoty
Asymptota bez směrnice - ABS
- Nechť . Přímka se nazývá asymptota bez směrnice (svislá asymptota) v bodě , jestliže
Asymptota se směrnicí - ASS
-
Nechť . Přímka se nazývá asymptota se směrnicí (asymptota v ) funkce , jestliže
-
Lineární funkce je asymptotou se směrnicí (asymptota v ), právě když
- , kde ,
- , kde .
Podobná věta platí také pro asymptotu v .
Postup při vyšetřování průběhu funkce
-
Z předpisu funkce
- určíme definiční obor funkce, příp. nulové body
- určíme paritu funkce (sudá resp. lichá)
- rozhodneme o spojitosti funkce v definičním oboru
-
Vypočítáme první derivaci funkce
- určíme definiční obor derivace, určíme nulové body derivace (body podezřelé z extrému)
- určíme intervaly monotonie (roste resp. klesá)
- klasifikujeme extrémy
-
Vypočítáme druhou derivaci
- určíme intervaly konkávnosti resp. konvexnosti funkce
- určíme inflexní body
-
Sestavíme tabulku dosavadních informací o funkci
- užitečné pro přehlednost
- určíme a zapíšeme hodnoty funkce ve význačných bodech (extrémy, inflexní body).
-
Určíme rovnice asymptot (ABS, ASS), pokud existují.
-
Nakreslíme graf funkce.
Navigace
Předchozí: Derivace funkce a její geometrický význam - Pravidla pro derivování funkcí, derivace složené funkce, derivace inverzní funkce, derivace elementárních funkcí Následující: Neurčitý integrál a metody jeho výpočtu Celý okruh: 1. Teoretické základy informačních technologií