Určitý integrál
- Existuje několik definic určitého integrálu:
- Cauchyův
- Newtonův,
- Riemannův (nejčastější) - zobecnění Cachyuova integrálu,
- Lebesgueův…
- Definice se liší množinou funkcí, pro které platí
- Na rozdíl od neurčitého integrálu, kde výsledkem je množina primitivních funkcí, je výsledkem určitého integrálu číslo, které můžeme interpretovat jako obsah plochy pod křivkou grafu funkce na intervalu
- určitý integrál uvažujeme na uzavřeném intervalu, na níž je funkce omezena
- říkáme určitý integrál od do
- Využití pro výpočet:
- obsahu plochy pod křivkou grafu (rovinného útvaru),
- délky křivek,
- objemy rotačních těles, pláště těles,…
- jiné aplikace ve fyzice, chemii
Poznámka
Idea výpočtu obsahu plochy pro vymezený úsek grafu:
- Úsek grafu rozdělíme na podintervalů stejné délky
- (obecně stejné délky mít nemusí)
- Pro každý interval můžeme uvažovat obdélník, jehož základna je dána dělením a výška je dána některou funkční hodnotou na daném podintervalu
- např. lokální maximum/minimum
- Odhad (aproximace) obsahu celé plochy spočítáme jako součet obsahů ploch jednotlivých obdélníků
- Je přitom zřejmé že, pokud vezmeme jako výšky jednotlivých obdélníků lokální maxima/minima, je tento odhad nepřesný
- Přesnější odhad získáme jemnějším rozdělením na více podintervalů (užších obdélníků)
Dělení intervalu
- Mějme uzavřený interval , dělením tohoto intervalu pak rozumíme konečnou množinu bodů , která splňuje
- prvky množiny nazýváme dělící body intervalu
- interval , nazýváme i-tý interval dělení
- Množina nazýváme zjemnění dělení , je-li
- každý dělící bod dělení je tak dělícím bodem dělení
Horní a dolní součet
-
Nechť funkce je omezená na intervalu a množina je dělení intervalu
-
Horní součet funkce vzhledem k intervalu dělení je číslo kde
-
s rostoucím se se horní součet funkce zmenšuje
-
Dolní součet funkce vzhledem k intervalu dělení je číslo
kde
- s rostoucím se se dolní součet funkce zvětšuje
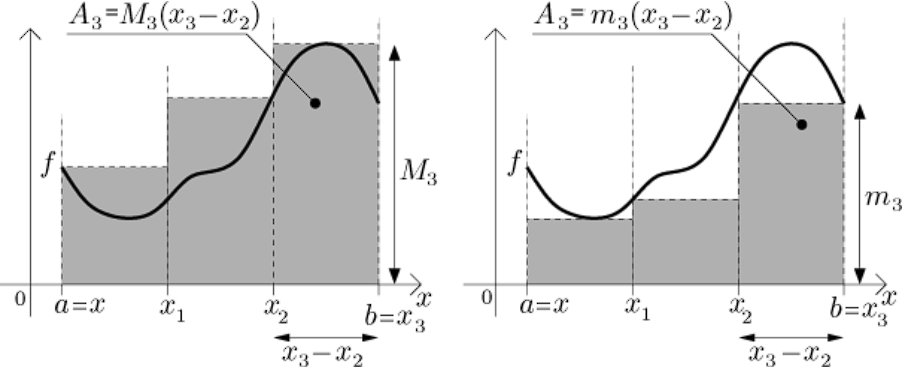
- Je zřejmé, že
- kde je skutečný obsah plochy pod grafem
- Zjemňováním dělení tak, že , dojde u horního součtu ke zmenšování, u dolního součtu ke zvětšování
- v obou případech se součty přiblíží k (splynou v jednu hodnotu)
- Této společné hodnotě , jestliže existuje, říkáme Riemannův integrál funkce od do
Horní a dolní integrál funkce
-
Existuje mnoho dělení intervalů na množině a můžeme uvažovat množinu všech horních součtů vzhledem k příslušným dělením
-
Zřejmě platí
-
je dolní závora funkce omezené na
- minimum z funkčních hodnot na intervalu
-
To znamená, že množina horních součtů je zdola omezená a existuje největší dolní mez těchto součtů. Číslo budeme nazývat horní Riemannův integrál funkce .
-
Dále můžeme podobně uvažovat množinu všech dolních součtů vzhledem k příslušným dělením intervalu , kterou označíme
-
Zřejmě platí
-
je nějaká horní závora omezené funkce na .
- maximum z funkčních hodnot na intervalu
-
To znamená, že množina dolních součtů je shora omezená a existuje nejmenší horní mez těchto součtů. Číslo budeme nazývat dolní Riemannův integrál funkce .
Riemannův integrál
- Říkáme, že definovaná a omezená na intervalu je Riemannovsky integrovatelná na právě tehdy, když
- horní a dolní Riemannovy integrály funkce jsou si rovny (dolní mez horních součtů a horní mez dolních součtů jsou si rovny)
- Krátce to budeme zapisovat jako
- Společná hodnota se pak nazývá Riemannův integrál a značí se což budeme jednoduše zkracovat jako
- číslo je nazývá dolní mez, pak horní mez (jedná se integrační meze)
Věty
- První věty jsou zjevné z toho, že zjemňováním se horní součet zmenšuje, dolní se naopak zvětšuje
- Horní součty jsou omezeny zdola a dolní shora, tyto meze jsou přitom rovny
-
Nechť je omezená na a je zjemnění dělení daného intervalu, pak
-
Je-li omezená na a jsou-li a libovolná dělení intervalu platí
-
Je-li definovaná a omezená na , pak .
-
Nechť je definovaná a omezená na . Pak právě tehdy, když pro libovolné existuje dělení intervalu takové, že
- pro každé kladné reálné číslo existuje takové dělení intervalu, že rozdíl příslušných horních a dolních součtů je
-
Je-li monotónní na , pak .
Stejnoměrná spojitost
- Funkce definovaná na je stejnoměrně spojitá, jestliže
-
Nechť je definovaná a spojitá na . Pak je na stejnoměrně spojitá.
-
Nechť je spojitá na . Pak .
- Funkce je integrovatelná na uzavřených spojitých intervalech
- Některé funkce s konečným počtem skokových nespojitostí však integrovatelné jsou
- Výjimkou jsou ale např. Dirichletovy funkce, které bodů nespojitostí mají příliš mnoho
Vlastnosti Riemannova integrálu
- Nechť , pak
- je-li pro , pak
Poznámka
- Nechť a , pak podle části (2) předchozí věty je také a předpisem
- je na intervalu definována funkce. Položíme ještě
- Nechť a , pak je spojitá na .
- Nechť je spojitá na , pak , je diferencovatelná na , a platí .
- je tedy primitivní k .
Newton-Leibnizova formule
- Následující věta umožňuje snadný způsob výpočtu určitého integrálu:
- Nechť je spojitá na a je libovolná primitivní funkce k na tomto intervalu, pak
- Integrál funkce na intervalu je rovno rozdílu:
- - funkční hodnota primitivní funkce v
- - funkční hodnota primitivní funkce v
- Pro výpočet určitého integrálu tedy stačí vypočítat primitivní funkci podobně jako neurčitého integrálu
-
- dosadit koncové body a
-
- provést rozdíl pravého od levého
-
- Formule lze dokázat pomocí Lagrangeovy věty o střední hodnotě spojitých funkcí
Metody výpočtu
- Analogické jako u výpočtu neurčitého integrálu
Metoda per-partes
- Nechť a jsou spojitě diferencovatelné funkce na , pak
Metoda substituce
- Nechť je spojitá na a spojitě diferencovatelná na . Pak kde a .
- Při substituci je třeba pamatovat na to, že při zavedení nové proměnné, je nutné změnit příslušně i integrační meze
navíc…
Po částech spojitá funkce
- Funkce se nazývá po částech spojitá na , jestliže existuje dělení intervalu a spojité funkce definované na taková, že pro , .
Nevlastní integrál 1. druhu
- Nechť je funkce omezená na a -integrovatelná pro libovolné . Jestliže existuje vlastní říkáme, že konverguje. V opačném případě říkáme, že daný integrál diverguje.
Nevlastní integrál 2. druhu
- Nechť je definována na a je -integrovatelná na pro .
- Jestliže existuje říkáme, že konverguje.
Navigace
Předchozí: Neurčitý integrál a metody jeho výpočtu Následující: Geometrická interpretace určitého integrálu Celý okruh: 1. Teoretické základy informačních technologií