Counting Sort
- Algoritmus třídění, který využívá jinou informaci než porovnávání
- Lze použít pouze pro třídění celých čísel
- Idea:
- - pole vstupní
- - pole výstupní
- - pole pomocné
- Složitost algoritmu v nejhorším případě:
- stabilní algoritmus počítání
Counting-Sort(A, B, k)
for i <- 0 to k
do C[i] <- 0
for j <- 0 to n-1
do C[A[j]] <- C[A[j]]+1 // C[i] obsahuje počet prvků v A rovných i
for i <- 1 to k
do C[i] <- C[i] + C[i-1] // C[i] obsahuje počet prvků v A <= i
for j <- n-1 downto 0
do B[C[A[j]]-1] <- A[j]
C[A[j]] <- C[A[j]]-1Výpočet složitosti v nejhorším případě
- řádek instrukcí.
- řádek instrukcí.
- řádek instrukcí.
- řádek instrukcí.
- Tedy složitost Counting Sort je v nejhorším případě .
- Je-li (tedy pro ), je poté složitost v nejhorším případě
Příklad
Radix Sort
- Používali operátoři mechanických třídiček děrných štítků
- Idea:
- Třídíme -místná čísla.
- Třídění proběhne v průchodech.
- V průchodu se čísla setřídí podle jejich poslední číslice,
- v podle předposlední,
- …
- Lze jej využít i na třídění textových řetězců, data ve tvaru rok-měsíc-den, …
- Složitost algoritmu v nejhorším případě:
Radix-Sort(A, d)
for i <- 1 to d
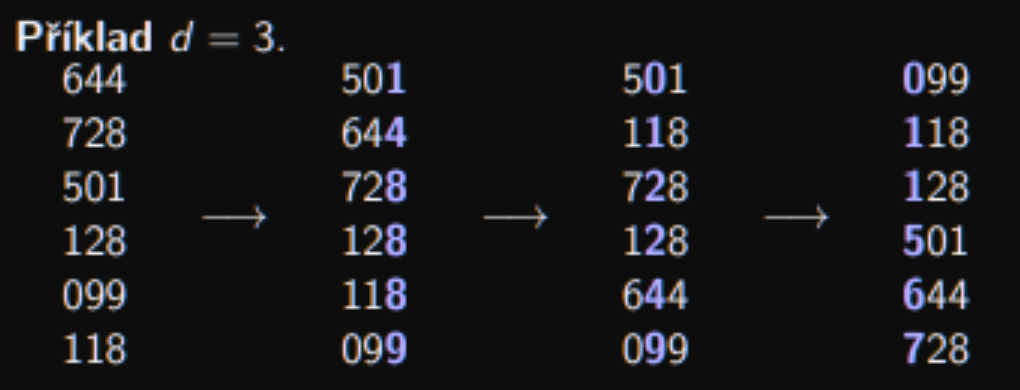
do Stable-Sort(A, i)Příklad
Výpočet složitosti v nejhorším případě
- řádek : instrukcí
- řádek instrukcí
Bucket Sort
- Třídí čísla z intervalu
- Idea:
- Projdeme prvky pole a každý z nich vložíme do příslušného intervalu (do příslušného seznamu ).
- Každý seznam setřídíme.
- Prvky setříděných seznamů vložíme po řadě do výstupního pole
- Složitost algoritmu v nejhorším případě je:
- Složitost v průměrném případě je
Bucket-Sort(A[0 ... n-1])
for i <- 0 to n-1
do vlož A[i] do seznamu B[floor(n*A[i])]
for i <- 0 to n-1
do Sort(B[i])
vlož postupně prvky z B[0], ..., B[n-1] do pole APříklad
Výpočet složitosti v nejhorším případě
- To je případ, když všechny prvky z byly umístěny do jednoho seznamu
- Složitost bucket Sortu tedy je:
Navigace
Předchozí: Heap sort a jeho složitost Následující: Pořádkové statistiky Celý okruh: 1. Teoretické základy informačních technologií