Průchod grafu
- Pro graf a počáteční vrchol , chceme systematicky navštívit všechny vrcholy dosažitelné z , každý z nich právě jednou.
- Vrchol je dosažitelný z , pokud existuje cesta z do .
Průchod do šířky a jeho vlastnosti
- Vstup:
- Graf
- Vrchol
- Projdeme vrcholy do kterých existuje cesta z
- Pomocné informace pro uzly v polích velikost , na indexu je informace k uzlu :
- color: barva uzlu, je to jedna z hodnot
white,gray,black - d: nejkratší vzdálenost od (vzdálenost je měřena jako počet hran ležících na cestě, nebo
- parent: rodič uzlu ve stromu, který průchodem vytváříme, nebo
nil
- color: barva uzlu, je to jedna z hodnot
Implementace
- Předpokládáme, že samotný graf je struktura s položkami
- V: množina vrcholů grafu (vhodně reprezentovaná)
- adj: reprezentace grafu pomocí seznamů sousedů
proc bfs(G, s)
foreach u in G.V - {s} // pres vrcholy grafu mimo s
color[u] = white
d[u] = ∞
parent[u] = nil
color[s] = gray
d[s] = 0
parent[s] = nil
Queue Q // fronta
enqueue(Q,s)
while !empty(Q)
u = dequeue(Q)
foreach v in G.adj[u] // pres sousedy vrcholu u
if color[v] == white
color[v] = gray
d[v] = d[u] + 1
parent[v] = u
enqueue(Q, v)
color[u] = blackAnalýza algoritmu
- Postupně objevujeme uzly:
- Neobjevené uzly mají barvu
white - Objevené uzly, o kterých nevíme, že mají objevené sousedy, mají barvu
gray - Objevené uzly, o kterých víme, že mají pouze objevené sousedy, mají barvu
black
- Neobjevené uzly mají barvu
- Složitost:
- Každý uzel je do fronty vložen pouze jednou (vkládáme pouze
whiteuzly, uzel je po vložení přebarven nagray) - Uzly do fronty vkládáme a z fronty je odebíráme v konstantním čase. Proto je složitost práce s frontou
- U každého uzlu po jeho odebrání z fronty projdeme seznam jeho sousedů. Víme ale, že součet délek seznamů v
adjje . Proto procházení seznamů zabere času - Celkem je tedy složitost
- Každý uzel je do fronty vložen pouze jednou (vkládáme pouze
Průchod do šířky
BFS(s) hledá uzly v pořadí podle vzdálenosti od
- Definice: Nejkratší vzdálenost z uzlu do uzlu je nejmenší počet hran, které má nějaká cesta z do .
- Pokud cesta z do neexistuje, pak .
Korektnost BFS
- Věta: Nechť je orientovaný nebo neorientovaný graf a . Potom na konci běhu algoritmu pro každý uzel platí:
- Existuje-li cesta z do , pak je
color[v]rovnoblack - Existuje-li cesta z do , pak je cesta, kterou sestavíme tak, že vezmeme nejkratší cestu z do
parent[v]a připojíme k ní hranu(parent[v], v), nejkratší cestou z do
BFS sestaví strom
- Předpokládejme, že máme (orientovaný nebo neorientovaný) graf a uzel a provedeme
bfs(G, s). Potom uvažujeme neorientovaný graf , kde - je strom s kořenem : z principu algortmu
bfsplyne, že (s přidáním každého uzlu mimo do fronty vytvoříme jednu hranu z ) a je souvislý (z každého uzlu vede cesta do , je to nejkratší cesta nalezenábfs) Uzel jako jediný nemá rodiče.
Průchod do hloubky a jeho vlastnosti
- Uzly mají položku pro barvu, podobně jako u průchodu do šířky. Možné barvy jsou opět
white,grayablack - Dále si pro každý uzel budeme zaznamenávat čas, kdy byl navštíven poprvé a změnil barvu z
whitenagray. K tomu použijeme položku . Dále zaznamenáme čas, kdy byl uzel navštíven podruhé, k tomu použijeme položku - Čas budeme udržovat pomocí globální proměnné
time, kterou na začátku nastavíme na , a na vhodných místech inkrementujeme
proc dfs(G)
foreach u in G.V
color[u] = white
parent[u] = nil
time = 0
foreach u in G.V
if color[u] == white
dfs-visit(G,u)proc dfs-visit(G, u)
time = time + 1
d[u] = time // prvni navsteva uzlu u
color[u] = gray
foreach v in G.adj[u] // navstivime vsechny nenavstivene sousedy u
if color[v] == white
parent[v] = u
dfs-visit(G,v)
color[u] = black
time = time + 1
f[u] = time // druha navsteva uzlu u- Složitost:
- Proceduru
dfs-visitvoláme pro každý uzel právě jednou - V rámci tohoto volání procházíme seznam sousedů. Součet délek všech seznamů sousedů je omezen .
- Zbytek procedury je v konstantním čase.
- Celkem je tedy složitost
- Proceduru
DFS sestaví les
- Předpokládejme, že proběhl
dfspro graf . Definujeme graf - je tvořen množinou stromů, je to tzv. les. Zdůvodnění je analogické tomu u
bfs. Stačí si všimnout, žedfs-visit(G,u)sestaví strom s kořenem - může být i jenom strom (= les s jedním stromem), například když je souvislý neorientovaný graf
- Lemma 4. Po provedení
dfspro každý uzel platí - Důkaz. Mezi první a druhou návštěvou uzlu vždy alespoň jednou inkrementujeme proměnnou
time
Průchod do hloubky
Topologické uspořádání
- Orientovaný graf bez cyklů budeme nazývat
dag. (to je zavedená anglická zkratka pojmu directed acyclic graph) - Topologické uspořádání dagu je lineární uspořádání vrcholů grafu takové, že pokud pak je v tomto uspořádání před
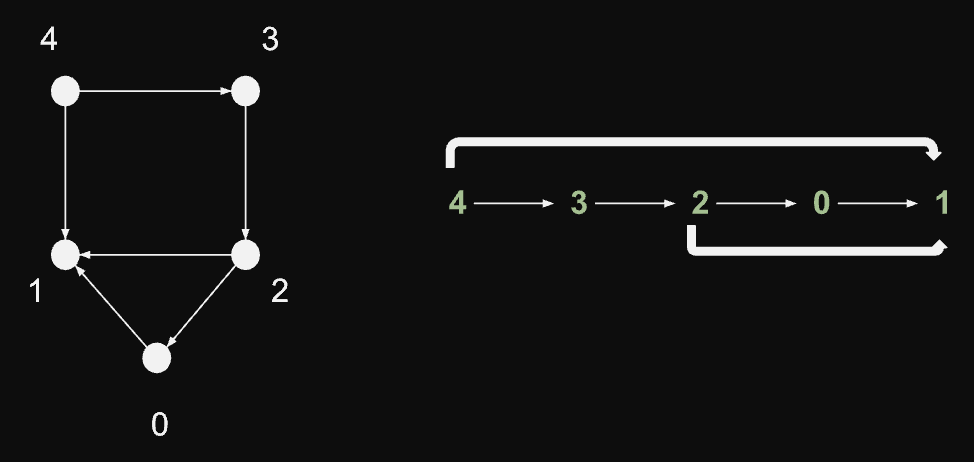
Algoritmus topol
-
Inicializujeme prázdný seznam uzlů
-
Spustíme upravený průchod do hloubky. Úprava spočívá v tom, že vždycky, když nastavujeme pro uzel , připojíme na začátek seznamu
-
Po skončení průchodu obsahuje seznam uzly uspořádané sestupně podle hodnot položky .
-
Složitost:
- Vkládání uzlu na začátek seznamu je v konstantním čase a vkládáme uzlů. To je jediná práce navíc oproti průchodu do hloubky. Proto je složitost
Navigace
Předchozí: Hashovací tabulky, metody řešení kolizí Následující: poslední Celý okruh: 1. Teoretické základy informačních technologií