Vlastnosti spojitých funkcí, spojitost složené a inverzní funkce

Spojitost funkce v bodě

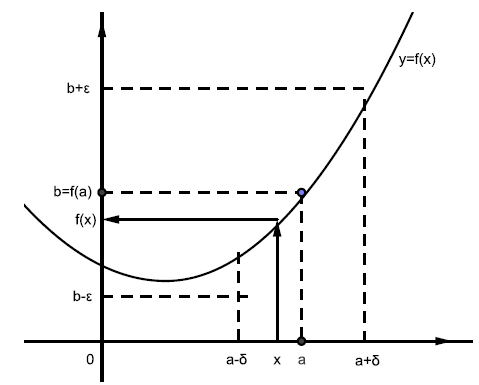
Říkáme, že $f : R \to R$ je spojitá v bodě $a \in R$ , právě když $lim_{x \to a} f (x) = f (a)$
Alternativní definice ( $ϵ - δ$ formulace spojitosti):
- Funkce $f$ definovaná na okolí bodu $a \in D_{f}$ je spojitá v bodě $a \in D_{f}$ , právě když pro každé $ϵ > 0$ existuje $δ > 0$ tak, že pro každé $x \in R$ splňující $∣ x - a ∣ < δ$ platí $∣ f (x) - f (a) ∣ < ϵ$ .
Analogicky říkáme, že $f$ je spojitá zprava resp. zleva, právě když $lim_{x \to a^{+}} f (x) = f (a)$ , resp. $lim_{x \to a^{-}} f (x) = f (a)$ .
Na rozdíl od limity:
- musí být funkce $f$ v bodě $a$ definována
- limita $lim_{x \to a} f (x)$ musí být rovna funkční hodnotě v bodě $a$

Nechť $f, g : R \to R$ . Pak:
1. $f$ je spojitá v bodě $a$ , právě když je v $a$ spojitá zprava i zleva
2. Jestliže je $f$ spojitá v $a$ , pak existuje $U (a)$ takové, že $f$ je omezená na $U (a)$
3. Jsou-li $f, g$ spojité v $a$ , pak $∣ f ∣$ , $f + g$ , $f \cdot g$ jsou také v $a$ spojité. Pokud $g (a) \neq = 0$ , je v $a$ spojitá i $\frac{f}{g}$
4. Nechť $f$ je spojitá v $a$ a $g$ spojitá v $A = f (a)$ . Pak je také $g \circ f$ spojitá v $a$

Nechť $f, g : R \to R$ a nechť:
- $lim_{x \to a} f (x) = A \in R$ ,
- $g$ je spojitá v $A$ .
Pak $lim_{x \to a} g (f (x)) = g (A)$ .

Nechť $f : R \to R$ , $x \in D (f)$ je elementární. Pak v každém bodě $x \in D (f)$ je $f$ spojitá.

Nechť $f$ je spojitá a ryze monotónní na intervalu $I$ . Pak inverzní funkce $f^{- 1}$ je také spojitá na $f (I)$ .

Je-li funkce $g$ spojitá v bodě $a$ a funkce $f$ spojitá v bodě $g (a)$ , pak je složená funkce $f \circ g$ spojitá v bodě $a$ .

Spojitost funkce na intervalu má zajímavé důsledky důležité pro vyšetření průběhu funkce

Nechť $f : R \to R$ je spojitá na uzavřeném intervalu $⟨ a, b ⟩$ . Pak:
1. O omezenosti: $f$ je omezená na $⟨ a, b ⟩$ .
2. O maximu a minimu: $f$ nabývá na $⟨ a, b ⟩$ svého (lokálního) maxima a minima.
  - To znamená, že existují $c, d \in ⟨ a, b ⟩$ takové, že $f (c) = min_{x \in ⟨ a, b ⟩} f (x)$ a $f (d) = max_{x \in ⟨ a, b ⟩} f (x)$
  - Což také znamená, že pro všechna $x \in ⟨ a, b ⟩$ je $f (c) \leq f (x) \leq f (d)$ .
  - Zjednodušeně, je-li funkce f spojitá v uzavřeném intervalu ⟨a,b⟩, pak nabývá v alespoň jednom bodě svého lokálního maxima a v alespoň jednom bodě svého minima.
  - Tato věta nám dává jistotu v existenci lokálního maxima a minima, neříká však nic o jejich vyhledání
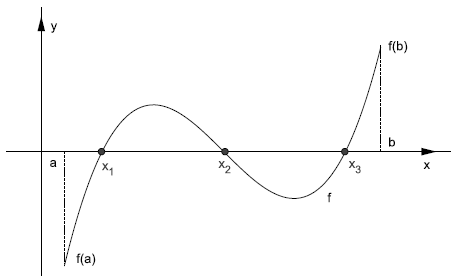
Nechť navíc $f (a) < f (b)$ . Pak: 3. O nabývání mezihodnot (Bolzanova-Weierstrassova věta): $f$ nabývá v intervalu $(a, b)$ všech hodnot mezi $f (a)$ a $f (b)$ .
- To znamená, že pro libovolné číslo $d \in (f (a), f (b))$ existuje číslo $c \in (a, b)$ takové, že $f (c) = d$ .

Nechť $f : R \to R$ je spojitá na uzavřeném intervalu $⟨ a, b ⟩$ taková, že $f (a) \cdot f (b) < 0$ . Pak existuje $c \in R$ takové, že $c \in (a, b)$ a $f (c) = 0$ .
- její graf v alespoň jednom vnitřním bodě tohoto intervalu protíná osu x
Jedná se o postačující podmínku, který je přímým důsledkem Bolzano-Weierstrassovy věty
- zajišťuje nám existenci nulového bodu
- nulový bod lze nalézt metodou půlení intervalu

Funkce $f$ je spojitá na uzavřeném intervalu $⟨ a, b ⟩$ a v $(a, b)$ nemá žádné nulové body, pak na $(a, b)$ je buď $f (x) > 0$ nebo $f (x) < 0$ pro všechny $x \in (a, b)$ .

Isibalo - Věty o spojitosti funkce

Isibalo - Cauchy-Bolzanova věta