Riemannův určitý integrál - definice, základní věta integrálního počtu, metody výpočtu

Určitý integrál

• Existuje několik definic určitého integrálu:
  • Cauchyův
  • Newtonův,
  • Riemannův (nejčastější) - zobecnění Cachyuova integrálu,
  • Lebesgueův…
• Definice se liší množinou funkcí, pro které platí
• Na rozdíl od neurčitého integrálu, kde výsledkem je množina primitivních funkcí, je výsledkem určitého integrálu číslo, které můžeme interpretovat jako obsah plochy pod křivkou grafu funkce $f$ na intervalu $⟨a,b⟩$
  • určitý integrál uvažujeme na uzavřeném intervalu, na níž je funkce $f$ omezena
  • říkáme určitý integrál $f$ od $a$ do $b$
• Využití pro výpočet:
  • obsahu plochy pod křivkou grafu (rovinného útvaru),
  • délky křivek,
  • objemy rotačních těles, pláště těles,…
  • jiné aplikace ve fyzice, chemii

Poznámka

Idea výpočtu obsahu plochy pro vymezený úsek grafu:

• Úsek grafu rozdělíme na $n$ podintervalů stejné délky
• (obecně stejné délky mít nemusí)
• Pro každý interval můžeme uvažovat obdélník, jehož základna je dána dělením a výška je dána některou funkční hodnotou na daném podintervalu
• např. lokální maximum/minimum
• Odhad (aproximace) obsahu celé plochy spočítáme jako součet obsahů ploch jednotlivých obdélníků
• Je přitom zřejmé že, pokud vezmeme jako výšky jednotlivých obdélníků lokální maxima/minima, je tento odhad nepřesný
  • Přesnější odhad získáme jemnějším rozdělením na více podintervalů (užších obdélníků)

Dělení intervalu

• Mějme uzavřený interval $⟨a,b⟩$, dělením tohoto intervalu pak rozumíme konečnou množinu bodů $D=\{x_0,x_1,...,x_n\}$, která splňuje $a=x_1<x_2<...<x_n=b$
  • prvky množiny $D$ nazýváme dělící body intervalu $⟨a,b⟩$
  • interval $⟨x_{i-1},x_i⟩$, $i\in \{1,2,...,n\}$ nazýváme i-tý interval dělení
• Množina $D^{{}^{\prime }}$ nazýváme zjemnění dělení $D$, je-li $D\subset D^{{}^{\prime }}$
  • každý dělící bod dělení $D$ je tak dělícím bodem dělení $D^{{}^{\prime }}$

Horní a dolní součet

• Nechť funkce $f$ je omezená na intervalu $⟨a,b⟩$ a množina $D$ je dělení intervalu $⟨a,b⟩$

• Horní součet funkce $f$ vzhledem k intervalu dělení $D$ je číslo $\overline{S}(f,D)={\sum }_{i=1}^n{M}_i(x_i-x_{i-1})$ kde $M_i=\sup \{f(x)\mid x_{i-1}\le x\le x_i\}$

• s rostoucím se $n$ se horní součet funkce $f$ zmenšuje

• Dolní součet funkce $f$ vzhledem k intervalu dělení $D$ je číslo

$$\underline{S}(f,D)=\sum _{i=1}^n{m}_i(x_i-x_{i-1}),$$

kde

$$m_i=\inf \{f(x)\mid x_{i-1}\le x\le x_i\}.$$

• s rostoucím se $n$ se dolní součet funkce $f$ zvětšuje

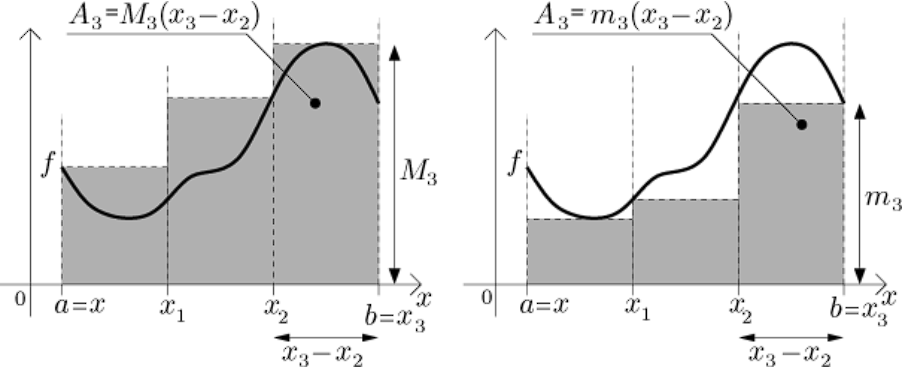
• Je zřejmé, že $\underline{S}(f,D)\le S(f,D)\le \overline{S}(f,D)$
  • kde $S(f,D)$ je skutečný obsah plochy pod grafem
• Zjemňováním dělení $D$ tak, že $n\to \infty$, dojde u horního součtu ke zmenšování, u dolního součtu ke zvětšování
  • v obou případech se součty přiblíží k $S(f,D)$ (splynou v jednu hodnotu)
• ${\lim }_{n\to \infty }{\sum }_{i=1}^n{m}_i(x_i-x_{i-1})=S(f,D)=li{m}_{n\to \infty }{\sum }_{i=1}^n{M}_i(x_i-x_{i-1})$
• Této společné hodnotě $S(f,D)$, jestliže existuje, říkáme Riemannův integrál funkce $f$ od $a$ do $b$

Horní a dolní integrál funkce

• Existuje mnoho dělení intervalů na množině $⟨a,b⟩$ a můžeme uvažovat množinu všech horních součtů vzhledem k příslušným dělením $U=\{\overline{S}(f,D)\mid D\text{ je deˇlenıˊ }⟨a,b⟩\}$

• Zřejmě platí $\overline{S}(f,D)\ge m{\sum }_{i=1}^n(x_i-x_{i-1})=m(b-a),$

• $m$ je dolní závora funkce $f$ omezené na $⟨a,b⟩$

  • minimum z funkčních hodnot na intervalu

• To znamená, že množina horních součtů je zdola omezená a existuje největší dolní mez těchto součtů. Číslo $\overline{S}=\inf U$ budeme nazývat horní Riemannův integrál funkce $f$.

• Dále můžeme podobně uvažovat množinu všech dolních součtů vzhledem k příslušným dělením intervalu $⟨a,b⟩$, kterou označíme $L=\{\underline{S}(f,D)\mid D\text{ je deˇlenıˊ }⟨a,b⟩\}$

• Zřejmě platí $\underline{S}(f,D)\le M{\sum }_{i=1}^n(x_i-x_{i-1})=M(b-a),$

• $M$ je nějaká horní závora omezené funkce $f$ na $⟨a,b⟩$.

  • maximum z funkčních hodnot na intervalu

• To znamená, že množina dolních součtů je shora omezená a existuje nejmenší horní mez těchto součtů. Číslo $\underline{S}=\sup L$ budeme nazývat dolní Riemannův integrál funkce $f$.

Riemannův integrál

• Říkáme, že $f:\mathbb{R}\to \mathbb{R}$ definovaná a omezená na intervalu $⟨a,b⟩$ je Riemannovsky integrovatelná na $⟨a,b⟩$ právě tehdy, když $\overline{S}=\underline{S}$
  • horní a dolní Riemannovy integrály funkce $f$ jsou si rovny (dolní mez horních součtů a horní mez dolních součtů jsou si rovny)
• Krátce to budeme zapisovat jako $f(x)\in \mathcal{R}(a,b)$
• Společná hodnota se pak nazývá Riemannův integrál a značí se $(R){\int }_a^{b}f(x)dx,$ což budeme jednoduše zkracovat jako ${\int }_a^{b}f(x)dx,$
• číslo $a$ je nazývá dolní mez, $b$ pak horní mez (jedná se integrační meze)

Věty

• První věty jsou zjevné z toho, že zjemňováním se horní součet zmenšuje, dolní se naopak zvětšuje
• Horní součty jsou omezeny zdola a dolní shora, tyto meze jsou přitom rovny

1. Nechť $f:\mathbb{R}\to \mathbb{R}$ je omezená na $⟨a,b⟩$ a $D_0$ je zjemnění dělení $D$ daného intervalu, pak $\underline{S}(f,D)\le \underline{S}(f,D_0)\le \overline{S}(f,D_0)\le \overline{S}(f,D).$

2. Je-li $f:\mathbb{R}\to \mathbb{R}$ omezená na $⟨a,b⟩$ a jsou-li $D_1$ a $D_2$ libovolná dělení intervalu $⟨a,b⟩$ platí $\underline{S}(f,D_1)\le \overline{S}(f,D_2).$

3. Je-li $f:\mathbb{R}\to \mathbb{R}$ definovaná a omezená na $⟨a,b⟩$, pak $\underline{S}\le \overline{S}$.

4. Nechť $f:\mathbb{R}\to \mathbb{R}$ je definovaná a omezená na $⟨a,b⟩$. Pak $f\in \mathcal{R}(a,b)$ právě tehdy, když pro libovolné $ϵ>0$ existuje dělení $D_{ϵ}$ intervalu $⟨a,b⟩$ takové, že $\overline{S}(f,D_{ϵ})-\underline{S}(f,D_{ϵ})<ϵ.$

   • pro každé kladné reálné číslo $ϵ$ existuje takové dělení intervalu, že rozdíl příslušných horních a dolních součtů je $<$ $ϵ$

5. Je-li $f$ monotónní na $⟨a,b⟩$, pak $f\in \mathcal{R}(a,b)$.

Stejnoměrná spojitost

• Funkce $f$ definovaná na $⟨a,b⟩$ je stejnoměrně spojitá, jestliže $\forall ϵ>0\exists \delta >0\forall x,y\in ⟨a,b⟩:(|x-y|<\delta )⟹|f(x)-f(y)|<ϵ).$

6. Nechť $f$ je definovaná a spojitá na $⟨a,b⟩$. Pak $f$ je na $⟨a,b⟩$ stejnoměrně spojitá.

7. Nechť $f$ je spojitá na $⟨a,b⟩$. Pak $f\in \mathcal{R}(a,b)$.

   • Funkce $f$ je integrovatelná na uzavřených spojitých intervalech
   • Některé funkce s konečným počtem skokových nespojitostí však integrovatelné jsou
   • Výjimkou jsou ale např. Dirichletovy funkce, které bodů nespojitostí mají příliš mnoho

Vlastnosti Riemannova integrálu

• Nechť $f,g\in \mathcal{R}(a,b)$, pak

1. ${\int }_a^b[\alpha f(x)+\beta g(x)]dx=\alpha {\int }_a^{b}f(x)dx+\beta {\int }_a^{b}g(x)dx,$
2. ${\int }_a^{b}f(x)dx={\int }_a^{c}f(x)dx+{\int }_c^{b}f(x)dx,a\le c\le b,$
3. je-li $f(x)\le g(x)$ pro $\forall x\in ⟨a,b⟩$, pak ${\int }_a^{b}f(x)dx\le {\int }_a^{b}g(x)dx,$
4. $\left|{\int }_a^{b}f(x)dx\right|\le {\int }_a^b|f(x)|dx.$
5. ${\int }_a^{b}f(x)=-{\int }_b^{a}f(x)$

Poznámka

• Nechť $f\in \mathcal{R}(a,b)$ a $x\in ⟨a,b⟩$, pak podle části (2) předchozí věty je také $f\in \mathcal{R}(a,x)$ a předpisem $F(x)={\int }_a^{x}f(t)dt$
• je na intervalu $⟨a,b⟩$ definována funkce. Položíme ještě $F(a)={\int }_a^{a}f(t)dt=0.$
• Nechť $f\in \mathcal{R}(a,b)$ a $F(x)={\int }_a^{x}f(t)dt$, pak $F$ je spojitá na $⟨a,b⟩$.
• Nechť $f$ je spojitá na $⟨a,b⟩$, pak $F(x)={\int }_a^{x}f(t)dt$, je diferencovatelná na $⟨a,b⟩$, a platí $F^{\prime }=f$.
  • $F$ je tedy primitivní k $f$.

Newton-Leibnizova formule

• Následující věta umožňuje snadný způsob výpočtu určitého integrálu:
• Nechť $f$ je spojitá na $⟨a,b⟩$ a $F$ je libovolná primitivní funkce k $f$ na tomto intervalu, pak ${\int }_a^{b}f(x)dx=F(b)-F(a).$
• Integrál funkce $f$ na intervalu $⟨a,b⟩$ je rovno rozdílu:
  • $F(b)$ - funkční hodnota primitivní funkce v $b$
  • $F(a)$ - funkční hodnota primitivní funkce v $a$
• Pro výpočet určitého integrálu tedy stačí vypočítat primitivní funkci podobně jako neurčitého integrálu
  • • dosadit koncové body $a$ a $b$
  • • provést rozdíl pravého od levého
• Formule lze dokázat pomocí Lagrangeovy věty o střední hodnotě spojitých funkcí

Metody výpočtu

• Analogické jako u výpočtu neurčitého integrálu

Metoda per-partes

• Nechť $F$ a $G$ jsou spojitě diferencovatelné funkce na $⟨a,b⟩$, pak ${\int }_a^{b}F(x)g(x)dx={\left[F(x)G(x)\right]}_a^b-{\int }_a^{b}f(x)G(x)dx.$

Metoda substituce

• Nechť $f$ je spojitá na $⟨a,b⟩$ a $g$ spojitě diferencovatelná na $⟨\beta ,\gamma ⟩$. Pak ${\int }_a^{b}f(x)dx={\int }_{\beta }^{\gamma }(f\circ g)(t)g^{\prime }(t)dt,$kde $g(\beta )=a$ a $g(\gamma )=b$.
• Při substituci je třeba pamatovat na to, že při zavedení nové proměnné, je nutné změnit příslušně i integrační meze

navíc…

Po částech spojitá funkce

• Funkce $f$ se nazývá po částech spojitá na $⟨a,b⟩$, jestliže existuje dělení $D=\{x_0,x_1,\dots ,x_n\}$ intervalu $⟨a,b⟩$ a spojité funkce $f_i$ definované na $⟨x_{i-1},x_i⟩$ taková, že $f(x)=f_i(x)$ pro $x\in ⟨x_{i-1},x_i⟩$, $i=1,2,\dots ,n$.

Nevlastní integrál 1. druhu

• Nechť je funkce $f$ omezená na $⟨a,\infty ⟩$ a $R$-integrovatelná pro libovolné $b>a$. Jestliže existuje vlastní ${\lim }_{b\to \infty }{\int }_a^{b}f(x)dx$ říkáme, že ${\int }_a^{\infty }f(x)dx$ konverguje. V opačném případě říkáme, že daný integrál diverguje.

Nevlastní integrál 2. druhu

• Nechť $f$ je definována na $⟨a,b⟩$ a je $R$-integrovatelná na $⟨a+ϵ,b⟩$ pro $0<ϵ<b-a$.
• Jestliže existuje ${\lim }_{ϵ\to 0^{+}}{\int }_{a+ϵ}^{b}f(x)dx$ říkáme, že ${\int }_a^{b}f(x)dx$ konverguje.

Navigace

Předchozí: Neurčitý integrál a metody jeho výpočtu Následující: Geometrická interpretace určitého integrálu Celý okruh: 1. Teoretické základy informačních technologií