- Třídění haldou (hromadou)
- Využívá datovou strukturu zvanou halda
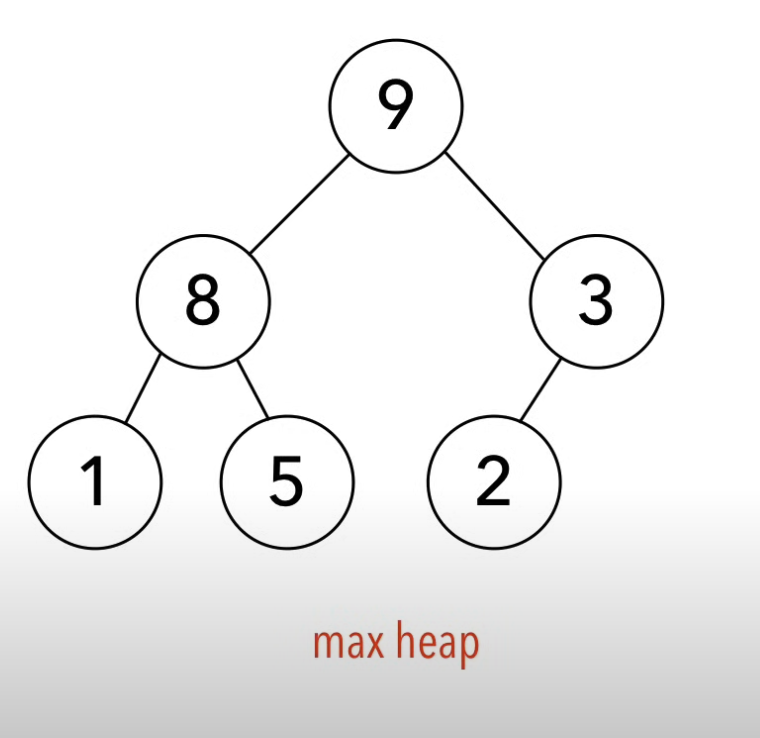
- (Binární) halda = pole, ve kterém uložení prvků simuluje jejich přirozené uložení v binárním stromu
- Složitost algoritmu v nejhorším případě:
- Pole se nazývá max-halda, pokud pro každý platí, že
- Pole se nazývá min-halda, pokud pro každý platí, že
- in-place třídění
- nestabilní algoritmus porovnávání
Princip algoritmu
- Algoritmus transformuje vstupní pole na binární max-haldu, kde každý rodičovský uzel má hodnotu větší než jeho děti.
- Toto uspořádání zajistí, že největší prvek je na vrcholu haldy.
- Algoritmus postupně odstraňuje největší prvek (kořen haldy) a vyměňuje ho s posledním prvkem v haldě.
- Pak znovu obnoví strukturu max-haldy ve zbytku pole a pokračuje, dokud nejsou všechny prvky setříděné.
Left(i)
return 2i+1Right(i)
return 2i+2Max-Heapify(A, i) // Podobné Build-Max-Heap, ale počítá s tím, že část pole
l <- Left(i) // již je setřízena
r <- Right(i) // O(log n)
if l <= heap-size(A) and A[l] > A[i]
then largest <- l
else largest <- i
if r <= heap-size(A) and A[r] > A[largest]
then largest <- r
if largest != i
then swap(A[i], A[largest])
Max-Heapify(A, largest)Build-Max-Heap(A[0 ... n-1]) // Vytvoří max-heap z nesetřízeného pole
heap-size(A) <- n // O(n)
for i <- floor(n/2)-1 downto 0
do Max-Heapify(A, i)Heap-Sort(A[0 ... n-1])
Build-Max-Heap(A)
for i <- n-1 downto 1
do swap(A[0], A[i])
heapsize(A) <- heapsize(A)-1
Max-Heapify(A, 0)Příklad
Odůvodnění složitosti Heap Sort
Navigace
Předchozí: Merge sort a jeho složitost Následující: Další metody třídění - counting sort, radix sort, bucket sort Celý okruh: 1. Teoretické základy informačních technologií