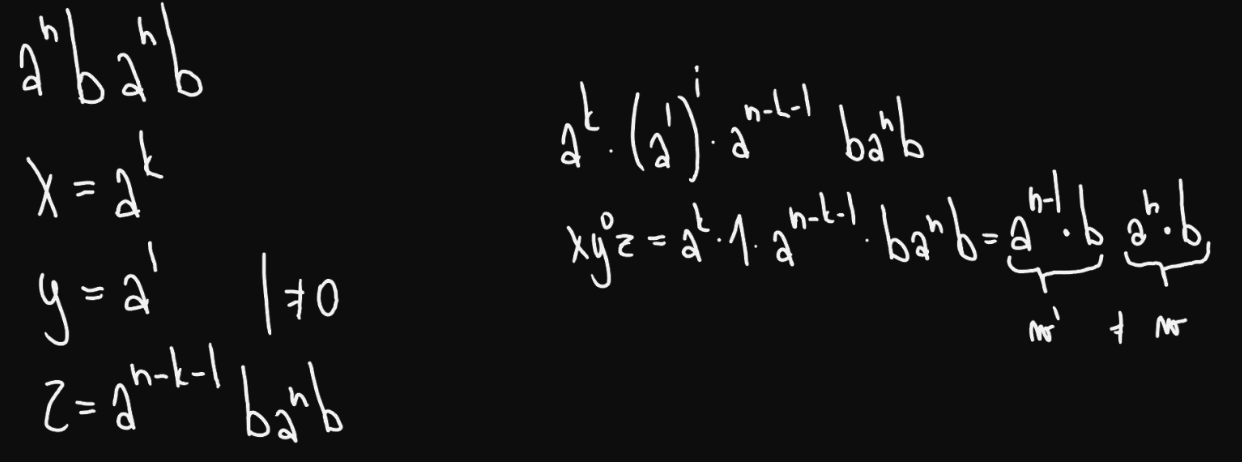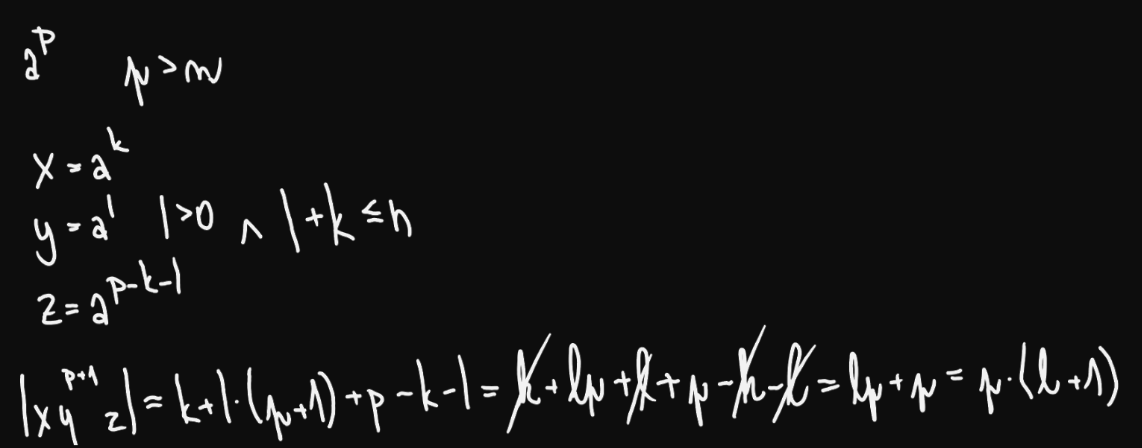Pumping lemma

Pumping lemma pro regulární jazyky

• Užitečný nástroj, který umožňuje dokázat, že daný jazyk není regulární (neumožňuje dokázat, že jazyk regulární je)

Definice

• Nechť $L$ je regulární jazyk, pak existuje číslo $n\in N$ tak, že každý řetězec $w\in L$ délky alespoň $n$ lze rozdělit na tři části $w=xyz$, které splňují
  1. $|y|>0$
  2. $|xy|\le n$
  3. $x{y}^{i}z\in L$ pro všechna $i\ge 0$
• pokud je jazyk $L$ konečný (a tedy i regulární), pak lemma platí triviálně - $n$ zvolíme větší než je délka nejdelšího řetězce v $L$

Postup při použití lemma v důkazu sporem

1. Předpokládáme, že daný jazyk je regulární a tedy musí existovat $n\in N$ z lemma

• (nikdy nevolíme konkrétní $n$, protože pokud $L$ není regulární, $n$ neexistuje)

2. Zvolíme vhodný řetězec $w$ takový, že $|w|\ge n$

• ($w$ je tedy nějak vyjádřeno pomocí $n$; opět nikdy nevolíme konkrétní řetězec!)

3. Ukážeme, že pro každé rozdělení $xyz=w$ splňující podmínky $1$ a $2$ z lemma existuje $i$ tak, že $x{y}^{i}z$ nelze napumpovat dle bodu $3$

Příklady

1. $L_1=\{ww\mid w\in \{a,b{\}}^{\ast }\}$
2. $L_2=\{a^p\mid p\text{ je prvocˇıˊslo}\}$
3. Dříve jsme tvrdili, že $\{0k1k\mid k\ge 1\}$ není regulární jazyk.

• Předpokládejme, že by byl
• Pak by existovalo $n$ pro pumping lemma
• Nechť $w=0n1n$.
• Můžeme psát $w=xyz$, kde $x$ a $y$ jsou v $0^{\ast }$ a $y\ne ϵ$
• Pak by ale $xyyz$ patřilo do $L$, ale $xyyz$ má víc $0$ než $1$.

Pumping lemma pro bezkontextové jazyky

Definice

• Nechť $L$ je bezkontextový jazyk, pak existuje číslo $n\in N$ tak, že každý řetězec $s\in L$ délky alespoň $n$ lze rozdělit na pět částí $s=uvxyz$, které splňují
  1. $|vy|>0$
  2. $|vxy|\le n$
  3. $u{v}^{i}x{y}^{i}z\in L$ pro všechna $i\ge 0$

• Intuice: $L$ je bezkontextový, proto existuje PDA P, který jej rozpoznává; pokud máme dostatečně dlouhý řetězec $s\in L$, pak se v něm musí nějaký podřetězec $v$ opakovat, přičemž $P$ si na zásobník uloží výskyty tohoto podřetězce, a později je může srovnat s výskyty jiného podřetězce $y$ (proto mezu počtem opakování $v$ a $y$ může být závislost). Zásobník umožňuje pouze LIFO přístup, a proto $P$ nemůže zároveň srovnávat výskyty více jak jedné dvojice; navíc řetězce ze zásobníku čteme v opačném pořadí, než byly uloženy (proto $L_1=\{ww\mid w\in \{a,b{\}}^{\ast }\}\text{ nenıˊ CFL, prˇitom }\{w{w}^R\mid w\in \{a,b{\}}^{\ast }\}\text{ je v CFL}$)

Navigace

Předchozí: Minimalizace konečného deterministického automatu Následující: Bezkontextové jazyky a jejich vlastnosti (uzávěrové vlastnosti, jednoznačnost) Celý okruh: 1. Teoretické základy informatiky